WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

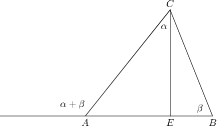
Re: Bewijs sin(a+b)=sinacosb+cosasinb

Dit is een reactie op vraag 86737

Ik snap niet goed waarom je zegt dat beide sinussen gelijk zijn aan CE/AC. En dat (alpha + bèta) gelijk is aan de hoek tussen AB (doorgetrokken bij A) en AC.
Stijn
Student Hoger Onderwijs België - dinsdag 28 augustus 2018

Antwoord

Bij $A$ heb je een gestrekte hoek, die is de som van de scherpe hoek bij $A$ in de driehoek en de stompe hoek links; de som van die twee hoeken is dus $\pi$.
Maar de som van de drie hoeken in de driehoek is ook $\pi$, daarom is de buitenhoek gelijk aan $\alpha+\beta$.
Voor die buitenhoek is $AC$ de schuine zijde en $CE$ de `overstaande' zijde; daarom is de sinus ook gelijk aan $CE/AC$.

kphart

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 29 augustus 2018