Re: Bewijs sin(a+b)=sinacosb+cosasinb

Dit is een reactie op vraag 86737

Ik snap niet goed waarom je zegt dat beide sinussen gelijk zijn aan CE/AC. En dat (alpha + bèta) gelijk is aan de hoek tussen AB (doorgetrokken bij A) en AC.

Stijn
Student Hoger Onderwijs België - dinsdag 28 augustus 2018

Antwoord

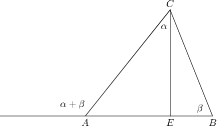
Bij A heb je een gestrekte hoek, die is de som van de scherpe hoek bij A in de driehoek en de stompe hoek links; de som van die twee hoeken is dus \pi.
Maar de som van de drie hoeken in de driehoek is ook \pi, daarom is de buitenhoek gelijk aan \alpha+\beta.
Voor die buitenhoek is AC de schuine zijde en CE de `overstaande' zijde; daarom is de sinus ook gelijk aan CE/AC.

kphart
woensdag 29 augustus 2018

©2001-2025 WisFaq