WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Eenheidscirkel

Hallo,

Hoe kan je met behulp van de eenheidscirkel sin ⁵/₆$\pi$
en cos 1¹/₆$\pi$ berekenen?

En een lastige waar ik niet uit kom: sin($\pi$+x)=-sin x
Ook met behulp van de eenheidscirkel.
Vriendelijk bedankt
Milou
Leerling bovenbouw havo-vwo - zaterdag 21 mei 2011

Antwoord

Ik ga uit van deze eenheidscirkel:

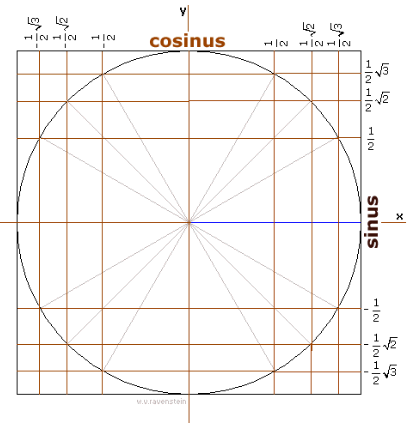
1.
sin ⁵/₆$\pi$:

Teken eerst een hoek van ⁵/₆$\pi$:

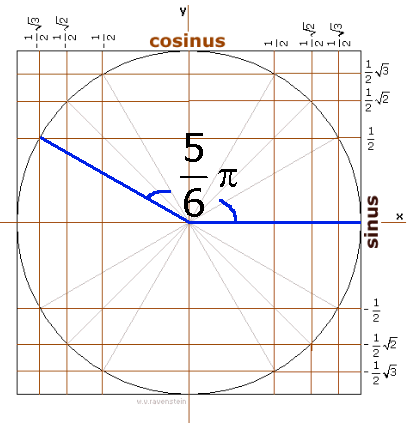
Je kunt dan 'rechts' de waarde van de sinus aflezen:

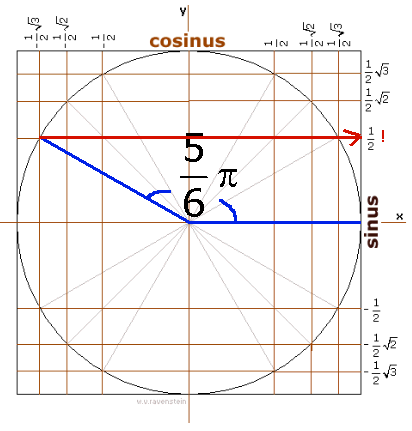
sin ⁵/₆$\pi$=¹/₂

2.
cos 1¹/₆$\pi$:

Eerst de hoek tekenen:

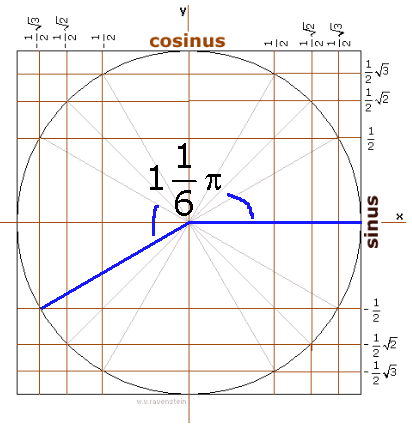
Nu kun je 'bovenaan' de waarde van de cosinus aflezen:

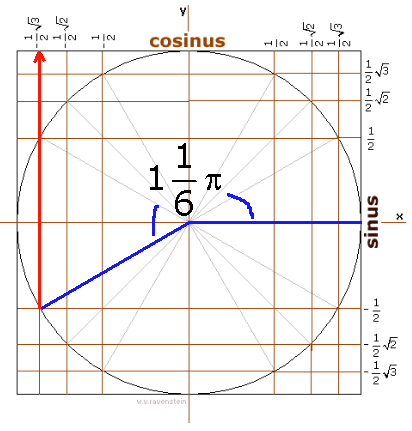
cos 1¹/₆$\pi$=-¹/₂√3

3.
Waarom is sin($\pi$+x)=-sinx?

Eerst maar 's een hoek tekenen van $\pi$+x:

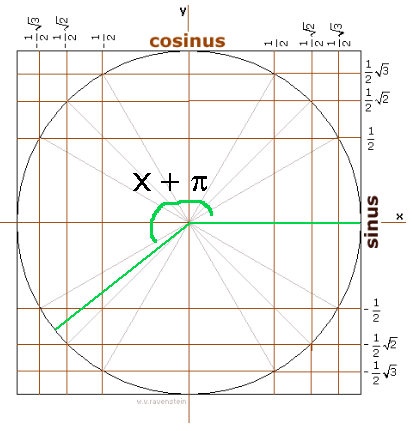
Waar zit 'x'?

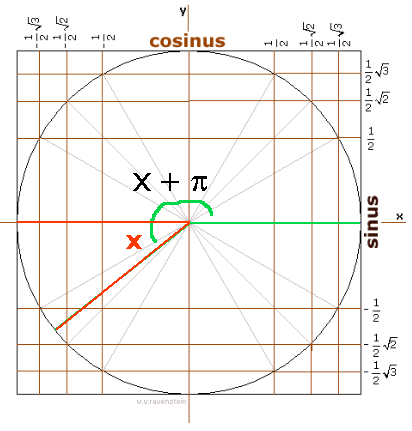
Je kunt 'rechts' de sinus aflezen:

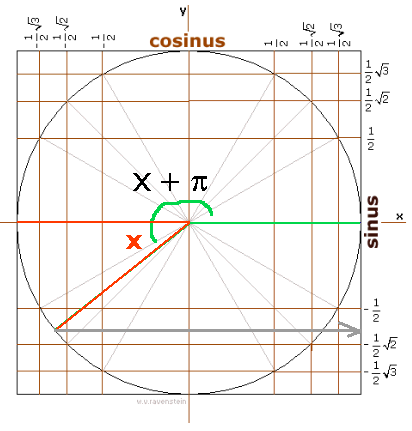
Je kunt ook rechts de -sin(x) aflezen en dat is precies hetzelfde:

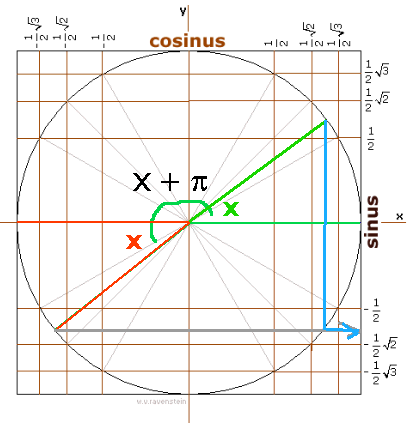
Het valt niet mee zo... maar hopelijk helpt het!

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 21 mei 2011

Re: Eenheidscirkel