De digitale vraagbaak voor het wiskundeonderwijs

home |  vandaag |  gisteren |  bijzonder |  gastenboek |  wie is wie? |  verhalen |  contact

HOME

samengevat
vragen bekijken
een vraag stellen
hulpjes
zoeken
FAQ
links
twitter
boeken
help

inloggen

colofon

   \require{AMSmath} Printen

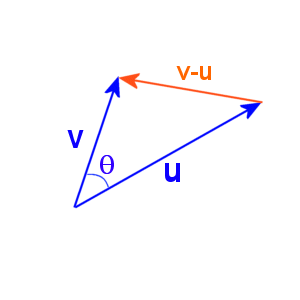
Hoek tussen 2 rechten

zoek bewijs/verklaring van formule welke de hoek geeft tssen 2 rechten. cos a = u . V / (||u|| . ||v||) , waarbij u en v 2 vectoren zijn v/d resp. rechten. Hoe komt men hiertoe?

Delphi
3de graad ASO - dinsdag 19 september 2006

Antwoord

we gaan uit van de cosinus-regel.
Deze luidt:

a2=b2+c2-2.b.c.cosa

Passen we deze regel toe op onderstaande situatieschets van twee vectoren u=(u1,u2) en v=(v1,v2) die een hoek q met elkaar maken:
q46700img1.gif

dan krijgen we:

|v-u|2 = u2+v2 - 2.|u|.|v|.cosq

Û
|u|.|v|.cosq = 1/2(|u|2+|v|2 - |v-u|2)
= 1/2(u12+u22+v12+v22 - (v1-u1)2-(v2-u2)2)
= ...
= u1v1+u2v2
= u·v

Zodoende is cosq = u·v/|u||v|

groeten,
martijn

mg
 Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 20 september 2006



home |  vandaag |  bijzonder |  gastenboek |  statistieken |  wie is wie? |  verhalen |  colofon

©2001-2025 WisFaq - versie 3