\require{AMSmath}

Domein en bereik

De verzameling van alle originelen heet domein en de verzameling van beelden heet bereik.

• Hoe vind je het domein?

  Meestal wordt het domein gegeven. Is dat niet het geval dan kunnen er problemen ontstaan in enkele van de volgende gevallen:

  • In het functievoorschrift komt een wortel voor.

    Het getal onder het wortelteken moet groter of gelijk zijn aan nul.

  • Er komt een deling voor in het functievoorschrift.

    Je kunt niet delen door nul. Zorg er voor dat het getal waardoor je deelt niet nul kan worden.

  • In het functievoorschrift staat een logaritme! ^glog(a) is alleen gedefinieerd voor a>0.
  • ...

• Hoe vind je het bereik?

  Kijk naar de mogelijke waarden die de functie aan kan nemen op het domein. Hiervoor teken je meestal de grafiek. Eventueel kun je maxima en minima uitrekenen. En let ook op asymptoten.

Intervalnotatie

Voorbeelden:

$[-3,4]$	alle getallen van -3 tot en met 4
$<-3,4]$	alle getallen tussen -3 en 4 of 4 zelf.
$<-5,\to>$	alle getallen groter dan -5
$[-5,\to>$	alle getallen groter of gelijk aan -5
<$\leftarrow$,$\sqrt{2}$]	alle getallen kleiner of gelijk aan $\sqrt{2}$

Voorbeeld

Opdracht	Oplossing	Grafiek
Gegeven is de functie: $f:x \to x^2-x$ Met Df = [-1,3>	De grafiek is een parabool. f(-1) = 2 f(3) = 6 Symmetrie-as: x = $\frac{1}{2}$ Minimum is f($\frac{1}{2}$) = $-\frac{1}{4}$
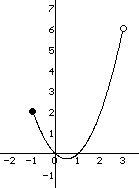Bepaal het bereik	Het bereik is [$-\frac{1}{4}$,6>	Wat kan y zijn ?

©2002-2007 WisWijzer

F.A.Q.

• Domein en bereik
• Domein en bereik
• Domein en bereik
• Domein en bereik

©2004-2024 WisFaq