De digitale vraagbaak voor het wiskundeonderwijs

home |  vandaag |  gisteren |  bijzonder |  gastenboek |  wie is wie? |  verhalen |  contact

HOME

samengevat

vragen bekijken

een vraag stellen

hulpjes

zoeken

FAQ

links

twitter

boeken

help

inloggen

colofon

Re: Hoe bereken je de tophoek van een regelmatige piramide

Dit is een reactie op vraag 47461

Beste

Ik snap dit stukje niet zo goed:
In 🔺️AQB:
AQ=√(x²+1/4x²+1/4x²)=√(3/2x²)=x√(3/2)
Hoe komt u aan die 1/4x² ?

Mvg

Emmi
2de graad ASO - zondag 2 augustus 2020

Antwoord

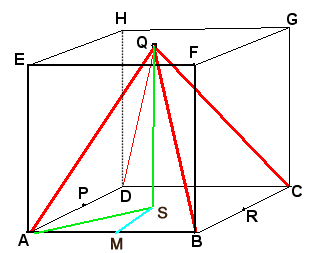
Er geldt:

\eqalign{ & AB = x \cr & AM = {1 \over 2}AB = {1 \over 2}x \cr & AS = \sqrt {AM^2 + MS^2 } = \sqrt {\left( {{1 \over 2}x} \right)^2 + \left( {{1 \over 2}x} \right)^2 } = \sqrt {{1 \over 4}x^2 + {1 \over 4}x^2 } \cr & AQ = \sqrt {AS^2 + SQ^2 } = \sqrt {{1 \over 4}x^2 + {1 \over 4}x^2 + x^2 } \cr}

Helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..! zondag 2 augustus 2020

home |  vandaag |  bijzonder |  gastenboek |  statistieken |  wie is wie? |  verhalen |  colofon

©2001-2025 WisFaq - versie 3