WisFaq!

Re: Hoe bereken je de tophoek van een regelmatige piramide

Beste

Ik snap dit stukje niet zo goed:
In 🔺️AQB:
AQ=√(x²+1/4x²+1/4x²)=√(3/2x²)=x√(3/2)
Hoe komt u aan die 1/4x² ?

Mvg

Emmi
2-8-2020

Antwoord

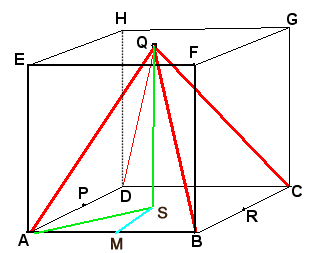
Er geldt:

$
\eqalign{
& AB = x \cr
& AM = {1 \over 2}AB = {1 \over 2}x \cr
& AS = \sqrt {AM^2 + MS^2 } = \sqrt {\left( {{1 \over 2}x} \right)^2 + \left( {{1 \over 2}x} \right)^2 } = \sqrt {{1 \over 4}x^2 + {1 \over 4}x^2 } \cr
& AQ = \sqrt {AS^2 + SQ^2 } = \sqrt {{1 \over 4}x^2 + {1 \over 4}x^2 + x^2 } \cr}
$

Helpt dat?

WvR
2-8-2020