WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Hoe bereken je de tophoek van een regelmatige piramide

In een kubus verbindt men het middelpunt van het bovenvlak met de 4 hoekpunten van het grondvlak. Hierdoor ontstaat een regelmatige piramide. Hoe groot is de cosinus van de tophoek $\alpha$?
Chris
3de graad ASO - donderdag 2 november 2006

Antwoord

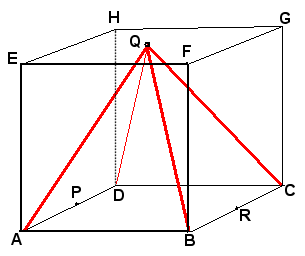
Kubus ABCD.EFGH , P is het midden van AD, Q is het midden van het bovenvlak, R is het midden van BC.
Stel de ribben hebben lengte x.

Het is even de vraag wat je precies onder 'tophoek' verstaat.
Versta je daaronder de hoek AQB? of de hoek PQR? Of hoek AQC?

Je kunt hier wellicht de cosinusregel voor driehoeken bij gebruiken:
a²=b²+c²-2bc.cos$\alpha$

Indien het gaat om hoek AQB:
AB=x
AQ=√(x²+¹/₄x²+¹/₄x²)=√(3/2 x²)=x√(3/2)
BQ=...=x√(3/2)
dus cos$\alpha$ = (3/2 x² + 3/2 x² - x²)/2.(3/2 x²) =
= 2/3

indien het gaat om hoek PQR:
PR=x
PQ=√(x²+¹/₄x²)= x√(5/4)
RQ= ... = x√(5/4)
dus cos$\alpha$ = ((5/4)x²+(5/4)x²-x²)/2.(5/4 x²)
= 3/5

indien het gaat om hoek AQC: ....
nou jij!

groeten,

martijn

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 3 november 2006

Re: Hoe bereken je de tophoek van een regelmatige piramide