|
|
|
\require{AMSmath}



Re: Driehoek delen in twee gelijke oppervlaktes
Is er een manier om (zonder zijden op te meten) met het programma CABRI klievers te construeren?
Alvast bedankt voor de moeite!
Paul
Leerling bovenbouw havo-vwo - zaterdag 25 november 2006
Antwoord
In het antwoord waarop je reageerde (Driehoek delen in twee gelijke oppervlaktes), is de constructie van een kliever (oppervlaktedeellijn) terug te vinden...
De punten P en Q liggen opvolgend op de zijden AB en AC van driehoek ABC, waarbij
AP = p . AB en AQ = q . AC en ook p.q =1/2
Wel, als je nu P willekeurig kiest op AB en de beide lengtes AP en AB meet (met de Cabri-functie 'Afstand'), dan kan je met Cabri's rekenmachine de waarde van p berekenen.
Met die zelfde Rekenmachine bereken je dan q, immers q = (1/2)/p.
En het punt Q is dan op AC te construeren met de functie 'Vermenigvuldiging' (selecteer eerst C, dan A en tenslotte de waarde van q).
Maar, je wilde niet meten...
En het kan zonder, maar dan moet je wel even wat herschrijven...
Je weet:
p = AP/AB en AQ / AC = q = (1/2) / p = (1/2) / (AP/AB) = AB / (2AP)
of anders geschreven:
AQ : AC = AB : 2AP
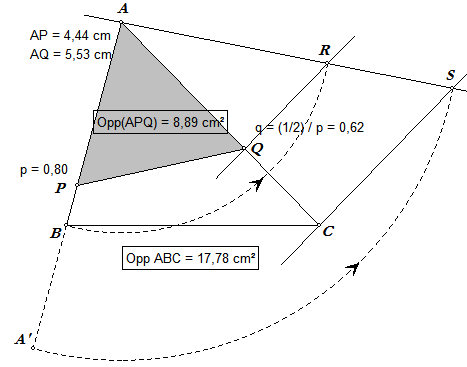
In bovenstaande figuur is die constructie weergegeven.
Op een willekeurig lijn door A ligt het punt R zo, dat AR = AB en het punt S zo, dat AS = 2AP (A' is de gespiegelde van A in het punt P).
Dan is de lijn SC getekend en vervolgens de lijn door R evenwijdig met SC.
Die laatste lijn snijdt AC in het gevraagde punt Q.
Ga zelf na waarom deze constructie juist is!
En dit alles dus bij een gegeven punt P op AB.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 25 november 2006
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 Dit is een reactie op vraag 9518
Dit is een reactie op vraag 9518 

