De punten P en Q liggen opvolgend op de zijden AB en AC van driehoek ABC, waarbij
AP = p . AB en AQ = q . AC en ook p.q =1/2
Wel, als je nu P willekeurig kiest op AB en de beide lengtes AP en AB meet (met de Cabri-functie 'Afstand'), dan kan je met Cabri's rekenmachine de waarde van p berekenen.
Met die zelfde Rekenmachine bereken je dan q, immers q = (1/2)/p.
En het punt Q is dan op AC te construeren met de functie 'Vermenigvuldiging' (selecteer eerst C, dan A en tenslotte de waarde van q).
Maar, je wilde niet meten...
En het kan zonder, maar dan moet je wel even wat herschrijven...
Je weet:
p = AP/AB en AQ / AC = q = (1/2) / p = (1/2) / (AP/AB) = AB / (2AP)
of anders geschreven:
AQ : AC = AB : 2AP
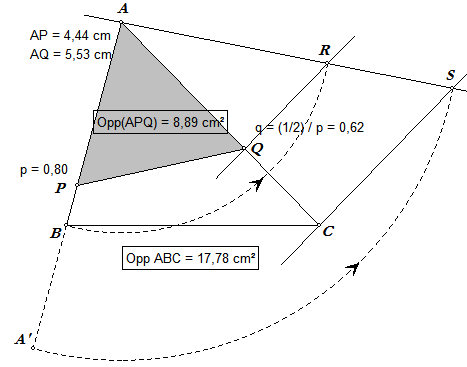
In bovenstaande figuur is die constructie weergegeven.
Op een willekeurig lijn door A ligt het punt R zo, dat AR = AB en het punt S zo, dat AS = 2AP (A' is de gespiegelde van A in het punt P).
Dan is de lijn SC getekend en vervolgens de lijn door R evenwijdig met SC.
Die laatste lijn snijdt AC in het gevraagde punt Q.
Ga zelf na waarom deze constructie juist is!
En dit alles dus bij een gegeven punt P op AB.
dk
25-11-2006