WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Driehoek delen in twee gelijke oppervlaktes

Op school hebben we het net gehad over het delen van een driehoek in twee stukken met een gelijke oppervlakte door een rechte lijn te trekken door een punt dat op de rand van de driehoek ligt.

Maar nu vroeg onze docent zich af of dit ook kon als alleen een willekeurig punt in de driehoek was gegeven. hij wist zelf ook nog niet hoe het moest en beloofde ons te belonen als wij wel wisten hoe het moest. Weten jullie of dit mogelijk is en hoe we dit dan kunnen doen of hoe we moeten beginnen met deze lijn te tekenen?

Ben
Leerling bovenbouw havo-vwo - zondag 6 april 2003

Antwoord

Vooraf (met dank aan Anneke Grunefeld en Jan Meerhof).
Zo zie je maar weer eens (als je het onderstaande verhaal leest) dat een leraar soms een vraag kan stellen, die tot verrassende resultaten kan leiden.

Eerst maar eens een analyse van het verkregen resultaat als P op AB ligt (een vervolg op jullie klasse-resultaat).

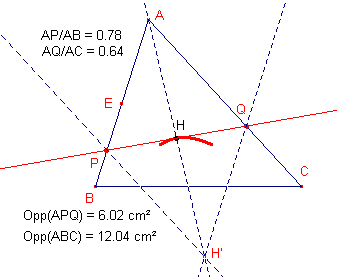
De "kliever" (van het werkwoord "klieven" = in twee stukken hakken) PQ deelt de oppervlakte van ABC in twee gelijke delen.
Volgens een bekende eigenschap is nu:
Opp(ABC) = ¹/₂.AB.AC.sin(A) = ¹/₂.bc.sin(A)
Stel nu dat P zo op AB ligt, dat AP/AB = p en Q zo, dat AQ/AC = q. Dan is evenzo:
Opp(APQ) = ¹/₂.AP.AQ.sin(A) = ¹/₂.pc.qb.sin(A)
Uit Opp(APQ)/Opp(ABC) = ¹/₂ volgt dan: pq = ¹/₂.
Op dit resultaat kan je dus eveneens een constructie van het punt Q baseren.
Dat is in bovenstaande tekening gedaan.
Daarbij hebben we aangenomen, dat P zo op AB ligt dat Q op AC ligt (en niet buiten de driehoek).
P ligt daardoor op EB (waarbij E het midden is van AB).

En dan volgt daaruit direct een bijzondere eigenschap.
We kiezen de drager van AB en de drager van AC als assen van een scheef coördinatenstelsel (met A als oorsprong).
p en q zijn dan de x- en y-coördinaten van de punten P en Q op deze assen. Zodat
P(p, 0), Q(0, q),
met verder ook
B(1,0) en C(0,1)
Het punt H' is het hoekpunt van het parallellogram APH'Q op AP en AQ.
H is het snijpunt van de diagonalen van diagonalen van dat parallellogram.

De meetkundige plaats van het punt H (bij verplaatsing van P op EB) is nu een deel van een hyperbool, waarvan AB en AC de asymptoten zijn.
Dit zouden we nog moeten bewijzen, maar het volgt min of meer uit het feit dat pq = ¹/₂.
Zie het kleine boogje in de figuur hierboven.
De lijn PQ is raaklijn in H aan deze hyperbool.
Men zegt ook wel dat deze hyperbool de "omhullende" is van de lijn PQ.

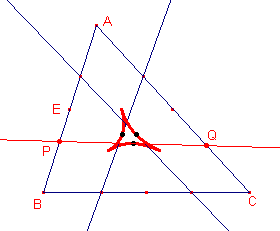
Op dezelfde manier kunnen we nog twee stukjes van twee andere hyperbolen vinden, nl. als we op dezelfde manier (als bij P) een punt kiezen op BC en ook op AC.
De zwaartelijnen uit A, B, C gaan door het gemeenschappelijk raakpunt van telkens twee van die hyperbolen.
De zwaartelijnen zijn immers ook "klievers".

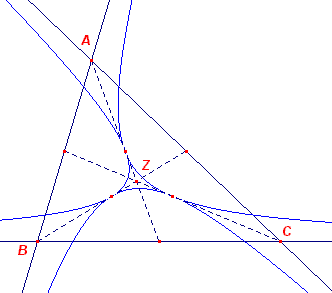
En dan volgt nu de oplossing van het probleem.
De gezochte "klievers" zijn raaklijnen aan zo'n hyperbool.
Duidelijk is, dat de drie hyperbolen afhankelijk zijn van de driehoek.
Bij een gegeven driehoek kunnen we de hyperbolen construeren (volgens de analytische meetkunde).
Dit valt echter buiten de lesstof op Nederlandse vwo-scholen (in Vlaanderen ook?).
Nb.
De raakpunten van telkens twee hyperbolen ("de keerpunten" in het tweede plaatje) zijn de middens van de zwaartelijnen van de driehoek.

Hebben we nu een punt dat binnen of buiten de driehoek ligt, dan is de kliever door dat punt een raaklijn aan zo'n hyperbool.

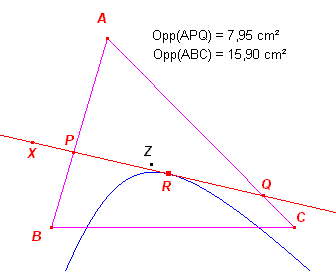
Overigens ook zo'n raaklijn is te construeren (dit gaat ook de vwo-lesstof te boven).
Niet moeilijk is nu in te zien, dat er door het zwaartepunt van de driehoek drie klievers gaan (de drie zwaartelijnen).
Door een punt (niet zijnde het zwaartepunt) binnen het hyperbolige driehoekje gaan ook drie klievers.
Er zijn twee oplossingen voor een punt op de zijden.En door alle andere punten gaat steeds één kliever.

Als ik het allemaal goed gezien heb...
En wie krijgt er nu een beloning?
Of hadden jullie of je leraar het zelf al gevonden?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 11 april 2003

Re: Driehoek delen in twee gelijke oppervlaktes