|
|
|
\require{AMSmath}



Algemene formule voor (a+b+c+d)n en de invulling van de lagen
Ik wil graag weten wat de algemene formule voor (a+b+c+d)n is. Zouden jullie me kunnen uitleggen hoe ik dit moet oplossen?
Tevens wil ik graag weten hoe je de getallen (rijen) die je uit het oplossen van de formule (a+b+c)n en (a+b+c+d)n krijgt, kunt invullen in de lagen van de piramide met respectievelijk een driehoek en vierkant als basis. (misschien een vierde dimensie?)
De getallen van (a+b+c)n die ik heb gekregen
zijn:
Rij 0 – 1
Rij 1 – 1 1 1
Rij 2 – 1 2 2 1 2 1
Rij 3 – 1 3 3 3 6 3 1 3 3 1
Rij 4 – 1 4 4 6 12 6 4 12 12 4 1 4 6 4 1
Ik zou dus graag willen weten hoe ik deze invul in de lagen, en dan met name het binnenste gedeelte.
Ook wil ik de grafische vorm (zeker) weten van zowel (a+b+c)n en (a+b+c+d)n, is dit een piramide met respectievelijk driehoek en een vierkant als basis?
Alvast bedankt,
Groeten,
JJ
Leerling bovenbouw havo-vwo - dinsdag 1 juni 2004
Antwoord
Volgens mij staan beide formules op Algemene formule voor (a+b+c)n (uitgebreid) en Binomium van newton (compacte vorm).
De driehoek van Pascal kan je opvatten als wandelingen in een rooster. Dus wat de grafische representatie betreft van de formule (a+b+c)n zou ik de multinomiaal coëffciënten eerder opvatten als wandelingen in een 3d-rooster dan in een piramide.
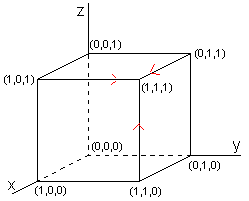
De vraag is dan natuurlijk hoe je je de M.C.'s van (a+b+c+d)n moet voorstellen..., maar dat laat ik graag aan de lezer over.
Zie Toepassingen van de piramide van Pascal

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 1 juni 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|











