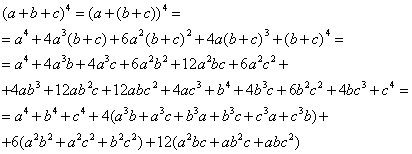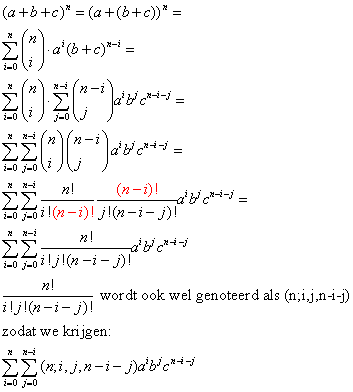WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Algemene formule voor (a+b+c)ⁿ

Ik wil graag weten wat de algemene formule voor (a+b+c)ⁿ is, als die bestaat. En zo niet zouden jullie me dan kunnen uitleggen hoe ik dit moet oplossen.

Alvast bedankt,

groetjes.
DK
Leerling bovenbouw havo-vwo - maandag 26 april 2004

Antwoord

Eerst maar eens een speciaal geval: (a+b+c)⁴:

Wat je ziet is dat b.v. de coefficienten voor a²bc, ab²c en abc² allemaal gelijk zijn aan 12.
Dat is niet zo verassend: het aantal volgordes van 2 a's een b en een c is natuurlijk hetzelfde als het aantal volgordes van 2 b's een c en een a.
Dit aantal volgordes is: 4!/(2!1!1!)

In het algemene geval krijg je allemaal termen van de vorm
a^pb^qc^n-p-q.
De coefficient voor zo'n term is dus n!/(p!q!(n-p-q)!).

Je kunt nu het algemene geval op een soortgelijke manier afleiden. Anders dan bij het binomium van Newton krijg je nu twee somtekens:

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 26 april 2004

De digitale vraagbaak voor het wiskundeonderwijs

Algemene formule voor (a+b+c)n

Antwoord

Algemene formule voor (a+b+c)ⁿ