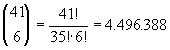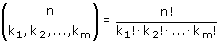WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Toepassingen van de piramide van Pascal

Vorige week had ik aan jullie een vraag gesteld over de toepassingen van de formule van de PIRAMIDE van Pascal. Toen vonden jullie voor mij een algebraische toepassing, waar ik erg veel mee kon. (nog heel erg bedankt ervoor!)

Maar nu vertelde mijn leraar dat er ook een toepassing bestaat die met combinatoriek/kansberekening te maken heeft. Hij gaf als voorbeeld een ketting met kralen van 3 verschillende kleuren. Maar ik snap nou niet hoe dat in elkaar zit. Kunnen jullie hiervan alsjeblieft een voorbeeld geven, en ook een uitleg/verklaring als dat kan..

Alvast heeel erg bedankt!
Joany
Leerling bovenbouw havo-vwo - dinsdag 30 april 2002

Antwoord

Het heeft even geduurd, maar ik geloof dat we er uit zijn. Bij telproblemen in de sfeer van "je kiest k elementen uit een verzameling van n elementen, waarbij ieder element hoogstens één maal wordt gekozen en waarbij niet gelet wordt op de volgorde" noemen we dat combinaties en daarbij gebruik je 'in feite' de driehoek van Pascal.

Voorbeeld
Bij de lotto worden iedere week zes lottogetallen getrokken, door achter elkaar zes balletjes uit een machine te laten rollen. Op iedere balletje staat een getal. De balletjes die er uit zijn gerold worden niet terug gestopt. De volgorde van de balletjes is niet belangrijk. Er zijn 41 balletjes en er worden zes balletjes getrokken.

Het aantal verschillende combinaties van 6 getallen uit 41 is:

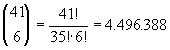
Voorbeeld
Je hebt een (open!) ketting met 7 rode, 4 witte en 3 blauwe kralen. Hoeveel verschillende kettingen kan je daarmee maken?

In toaal zijn er 14! verschillende permutaties te maken, maar dan tel je heel wat 'dezelfde' mogelijkheden dubbel.

Als je alleen kijkt naar de rode kralen zijn er steeds 7! kettingen hetzelfde (je kunt immers het verschil tussen de rode kralen niet zien). Hetzelfde geldt voor de witte (4!) en de blauwe (3!)..., dus je moet 14! delen door 7!, 4! en 3!

Het aantal kettingen is: 14!/(7!·4!·3!)=120120

Maar dit is precies de formule van Piramide van Pascal!

Overgens is dit 'gedoe' beter bekend onder de naam multinomiaalcoëfficiënt. Het aantal verschillende verdelingen van n elementen in m delen is:

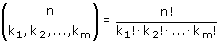
Zie ook:
vraag 839
vraag 2789

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 4 mei 2002