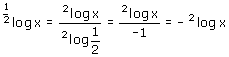|
|
|
\require{AMSmath}



Logaritmische vergelijking oplossen
2log(x+3)=1+1/2log x
wordt als volgt opgelost:
2log(x+3)=2log2-2logx
hoe maakt men van 1+1/2logx dan 2log2-2logx?
alvast bedankt
art
Leerling bovenbouw havo-vwo - maandag 26 januari 2004
Antwoord
Dit zijn eigenlijk 2 vragen.
1. Hoe kom je van 1 naar 2log2?
2. Hoe kom je van 1/2logx naar -2logx?
Het antwoord is (zoals altijd) het op het goede moment toepassen van de rekenregels.
1.
Ik wil alles 'in' dezelfde logaritme zetten dus ook de getallen uit de vergelijking. Ik zoek dus een b zodat 2logb=1, maar dan geldt: b=21=2, dus:
1=2log2 (L1)
2.
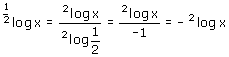
(L2 )
Zie ook: Logaritmische vergelijking

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 26 januari 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|