WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Logaritmische vergelijking

Ik heb de volgende vergelijking die ik moet oplossen maar ik kom er niet helemaal uit:

³logx + ^¹/₃log(x+b) = ⁹log(x-2)

Ik heb het volgende als eerste gedaan:

³logx - ³log(x+b) = ⁹log(x-2)
³log(x/(x+b)) = ⁹log(x-2)

nu moet ik volgens mij van die ⁹log(x-2) ook een ³log maken om ze tegen elkaar weg te strepen maar hoe doe ik dat.

Alvast bedankt.
Jelle
Student hbo - dinsdag 13 januari 2004

Antwoord

Twee manieren:

Beetje ingewikkeld...
Laten we zeggen dat ⁹log(x-2)=b, dan wil dat zeggen dat:
9^b=x-2

Omdat je eigenlijk ³log wilt zou je x-2 moeten schrijven als een macht van 3:

(3²)^b=x-2
3^2b=x-2

We zien: ³log(x-2)=2b
Dus ⁹log(x-2)=¹/₂·³log(x-2)

Keep it simple...
Rekenregel L2
Zie Rekenregels machten en logaritmen

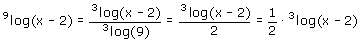
..dat is handiger...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 13 januari 2004