WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Integreren

Examenvraag

hallo, ik heb eigenlijk veel moeite met dit integraal (1/(1-x)).( $\sqrt{}$ (x/1-x)dx, ik heb al geprobeerd om substitutie te doen op verschillende manieren maar ik kom altijd in dezelfde loop waar ik nooit op een uitkomst komt
Annick
2-1-2025

Antwoord

Zo te zien gaat het om
$$\int\frac1{1-x}\cdot\sqrt{\frac{x}{1-x}}\,\mathrm{d}x
$$Maak daar eens
$$\int \sqrt{x}\cdot\frac1{(1-x)^{\frac32}}\,\mathrm{d}x
$$van. Doe een stap partiële integratie:
$$\sqrt{x}\cdot\frac2{\sqrt{1-x}}-\int\frac1{\sqrt{x}}\cdot\frac1{\sqrt{1-x}}\,\mathrm{d}x
$$De overgebleven integraal wordt nu
$$\int\frac1{\sqrt{x-x^2}}\,\mathrm{d}x
$$Je kunt $x-x^2$ omschrijven tot $\frac14-(x-\frac12)^2$, en dan is het een kwestie van herkennen: iets als $1/\sqrt{a^2-x^2}$ heeft een primitieve waar de arcsinus in zit. In dit geval krijg je
$$\int\frac1{\sqrt{x-x^2}}\,\mathrm{d}x =\arcsin(2x-1)
$$Bij elkaar genomen krijgen we dus
$$2\sqrt{\frac{x}{1-x}}-\arcsin(2x-1)
$$
kphart
3-1-2025

Wentelen om y-as van een NIET-functie

Geachte,graag uw hulp.
De opgave is deze: bereken de inhoud van het omwentelingslichaam rond de y-as van het ingesloten gebied bij y²= x²-x³
Ik begrijp dat de grafiek bestaat uit 2 takken: y=+/- $\sqrt{}$ (x²-x³)
Bij de pluswortel heb ik de top bepaald. Die zit bij x=2/3 en de bijbehorende y-waarde = $\sqrt{}$ (4/27). Maar verder kom ik eigenlijk niet. Ik zie echt niet hoe ik die 2 ' halve cirkeltjes ' kan wentelen om de x-as.
Ik begrijp ook dat ik de formule onder de integraal x²=y²-y³ moet gebruiken.
Maar hoe? Welke grenzen???

Bij voorbaat dank voor uw antwoord.
Dian
20-2-2025

Antwoord

Je begin met wentelen om de $y$-as, en later wil je om de $x$-as draaien. En omdat je $y=\pm\sqrt{x^2-x^3}$ schrijft denk ik dat het om de $x$-as moet. Kijk naar het plaatje

Als je die kromme om de $x$-as wentelt krijg je hetzelfde lichaam als wanneer je alleen de bovenkant wentelt. Maar dan is het makkelijk want je moet het kwadraat van de wortel integreren en er komt gewoon
$$
\pi\int_0^1 x^2-x^3\,\mathrm{d}x
$$

Een andere reden waarom ik denk dat er niet om de $y$-as gewenteld zal worden is dat je dan $x$ (of $x^2$) in $y$ moet uitdrukken; dat kan met behulp van de formules van Cardano, maar die geven niet echt een mooie uitdrukking om te integreren:
$$
x=\frac13+\frac16\sqrt[3]{8-108y^2+12\sqrt{81y^4-12y^2}}+ \frac16\sqrt[3]{8-108y^2-12\sqrt{81y^4-12y^2}}
$$
En dat beschrijft alleen nog maar het rechterstuk van de `waterdruppel', voor $x$ tussen $\frac23$ en $1$.
kphart
21-2-2025

Re: Wentelen om y-as van een NIET-functie

Geachte,
Hartelijk dank voor uw snelle antwoord. Voor alle duidelijkheid: er moet toch gewenteld worden om de y-as (Sorry voor het foutje in mijn vraag...)

De opdracht was om het 'begrensde' gebied te wentelen om de y-as. (Ik ging uit van de 2 gebieden in de 2 'waterdruppels'; ik zie niet welke andere gebieden er anders bedoeld zouden zijn) Het antwoord zou 64/105 $\pi$ zijn volgens het antwoordblad...

Waarom kan ik niet gewoon x en y verwisselen en dan gebruiken x²=y²-y³? Maar hoe zit het dan met de grenzen???

Nogmaals hartelijk dank!
Dian
21-2-2025

Antwoord

Het verwisselen van $x$ en $y$ betekent dat je het gebied spiegelt in de lijn $y=x$, en als je dat doet moet je dat gebied om de $x$-as draaien en dat betekent dat je de vergelijking naar $y$ moet oplossen, met dezelfde ingewikkelde formule als resultaat.

De opgave wordt een stuk makkelijker door poolcoördinaten te gebruiken. We voeren even een derde coördinaat $z$ in en drukken de kromme uit in $x$ en $z$ door $z^2=x^2-x^3$. Als de die om de $z$-as (die staat loodrecht op het $xy$-vlak) draaien. Je krijgt dan dit:

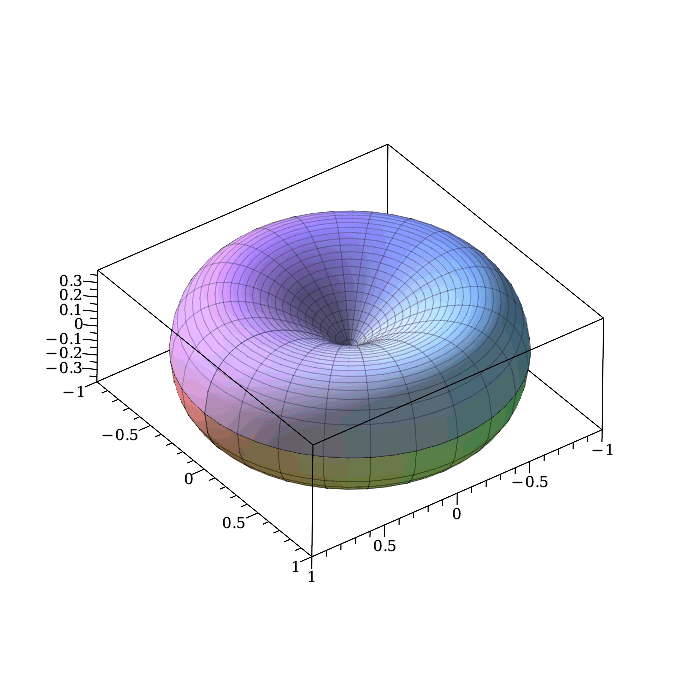
De vergelijking van het oppervlak is dan $z^2=(x^2+y^2)-(x^2+y^2)^{\frac32}$, en in poolcoördinaten wordt dat $z^2=r^2-r^3$ (want $x=r\cos\theta$, en $y=r\sin\theta$).
In de beschrijving loopt $\theta$ helemaal rond: $0\le\theta\le2\pi$, en voor $r$ geldt $0\le r\le1$, en voor $z$ komt er $-\sqrt{r^2-r^3}\le z\le\sqrt{r^2-r^3}$.
De inhoud van het wentellichaam wordt dan
$$
2\pi\cdot\int_0^12\sqrt{r^2-r^3}\cdot r\,\mathrm{d}r
$$
Omdat $r$ positief is kun je er deze integraal van maken: $4\pi\int_0^1r^2\sqrt{1-r}\,\mathrm{d}r$ en die levert inderdaad het antwoord dat je noemt.
kphart
22-2-2025

Laplace

Ik heb een dubbele integraal met variabelen x en y
functie: 1 / pi · e^-(x²+y²)

bovengrens x: - (√2 / 4)
ondergrens x: - (√(8)
bovengrens y: + (√(8)
ondergrens y: + (√2 / 4)

ik wil deze niet oplossen met polar coordinaten, maar met laplace.
is dat mogelijk met deze grenzen?

oplossen met substitutie : y=xt met t=y/x en dy/dt=x en dus dy=xdt
grenzen: t=-2 en t=-¹/₈

is dit correct?

gr, Jan

Herman
12-3-2025

Antwoord

Niet correct: $t$ loopt van $-8$ tot $-\frac18$. En ik zie nog niet wat de grenzen voor $x$ zijn bij vaste $t$. En hoe ziet de functie eruit die je gaat integreren?

kphart
12-3-2025

Dubbele integraal opstellen mbv poolcoördinaten

ik, heb moeite om de grenzen van theta te vinden bij deze specifieke opgave, zou iemand kunnen helpen?

(3 punten) Beschouw het gebied G ingesloten tussen de
Y-as en de kromme met vergelijking 2·x= -y²+4·y

Bereken de oppervlakte van dit gebied door de integraal te schrijven in poolcoördinaten als

opp(G)=∫ab(∫cdF(r,θ) dr)dθ
opp(G)=∫

i. Geef de grenzen voor de integraal over r
r: ______
ii. Geef de grenzen voor de integraal over θ
θ: ______
iii. Geef de numerieke uitkomst van de integraal: ______
Seppe
16-3-2025

Antwoord

i) substitueer $x=r\cos\theta$ en $y=r\sin\theta$ in de vergelijking herschrijf het resultaat in de vorm $r=\ldots$; dit geeft de bovengrens voor $r$, de ondergrens is makkelijk.

ii) de bovengrens is $\frac\pi2$; voor de ondergrens bereken je de helling van de parabool in het punt $(0,0)$.

iii) dit zou niet moeilijk moeten zijn met een geschikt programma, Maple bijvoorbeeld
kphart
16-3-2025

Wentelen om de y-as

de opdracht is: Het vlakdeel V wordt ingesloten door de grafiek van y= $\sqrt{}$ 2x-4, de x-as, y-as en de lijn y=3. Bereken exact de inhoud van het lichaam M dat ontstaat als V wentelt om de x-as. Hierbij gebruiken ze de inhoud van een cilinder ondanks dat het wentelen om de x-as is en niet om de y-as. Waarom?
Robin
6-4-2025

Antwoord

Er is een cilinder die hier een rol speelt. Teken het gebied, je zult zien dat het binnen de rechthoek ligt met basis het interval $[0,6\frac12]$ en hoogte $3$, en boven de grafiek van $y=\sqrt{2x-4}$.
Het gezochte wentellichaam is de cilinder met straal $3$ en lengte $6\frac12$, met daaruit het wentellichaam van $y=\sqrt{2x-4}$ weggesneden. De inhoud van de cilinder speelt hier dus een rol.

kphart
6-4-2025