|
|
|
\require{AMSmath}
Limiet berekenen
Dag
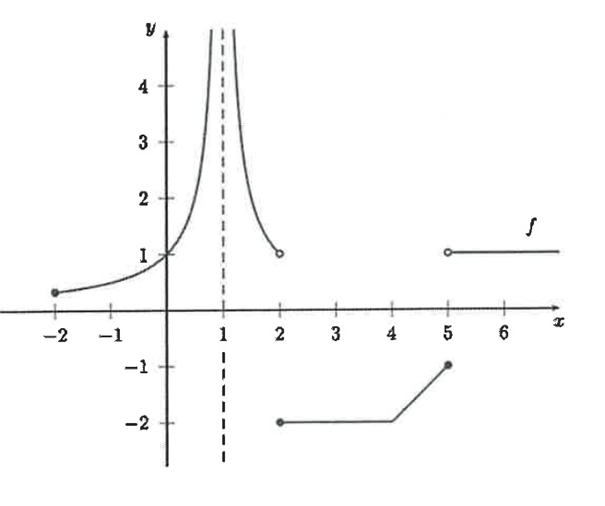
Gebaseerd op de grafiek (in bijlage):
limiet f(x) = -f(5) als x- $>$ 0 : waar of vals?
Het antwoord is blijkbaar waar, wat ik niet snap.
Dank voor wat uitleg.
Eugenie
eugenie
Student Hoger Onderwijs België - dinsdag 24 december 2024
Antwoord
Hallo Eugenie,
Zo te zien, is f(5)=-1. Immers, het dichte bolletje aan het eind van het deel van de grafiek tussen x=2 en x=5 geeft aan dat dit punt tot de grafiek behoort. Het open bolletje aan het begin van het meest rechter deel van de grafiek geeft aan dat dit deel van de grafiek nog niet geldt voor x=5, wel voor x $>$ 5.
Als f(5)=-1, dan is -f(5)=1.
Bij x=0 snijdt de grafiek de verticale as op hoogte 1, dus de limiet van f(x) voor x naar 0 is 1, net als -f(5). Het is dus waar dat deze limiet gelijk is aan -f(5).
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 24 december 2024
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3
|
Re: Limiet berekenen