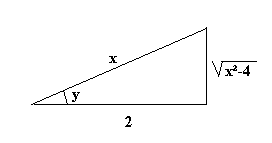WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Onbepaalde integraal bepalen met goniometrische functies

Geachte,

Ik ben een poging aan het doen volgende integraal aan het oplossen met een goniometrische functie

òdx/(x²·Ö(x²-4))

deze integraal is van de vorm:

òdx/(x²·Ö(x²-1))
en deze is oplosbaar via een eenvoudige substitutie
x = 1/cos(y) = sec (y) Þ dx = siny/cos²(y) dy

zodat Öx²-1 gelijk is aan sin y/cos y
de standaardintegraal gelijk is aan sin y + C zodat deze gelijk is aan Ö(x²-1)/x

desondanks vinden we onze eerste integraal niet via deze methode.

graag hulp, dank bij voorbaat

Iene
Iene R
Student universiteit België - dinsdag 9 november 2010

Antwoord

Hallo

Gebruik voor dergelijke integralen een driehoekje :

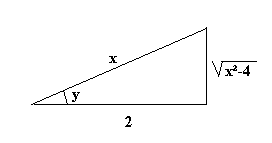
cos(y) = ²/_x
Dus x = ²/_cos(y)

dx = ^2.siny/_cos²y.dy

tan(y) = ^Ö(x²-4)/₂

dus Ö(x²-4) = 2.tan(y) = 2.^sin(y)/_cos(y)

En met dezelfde standaardintegraal bekom je dan :

^Ö(x²-4)/_4x

Ok?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 9 november 2010