WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Optimaliseren

Hallo,

Ik heb een som waar ik helemaal niet uit kom:

Gegeven zijn de functies f (x) = x e °·⁵x en g ( x ) = e °·⁵ x - 2.
Verder is gegeven dat de lijn x = p snijdt de grafiek van f in het punt A en de grafiek van g in punt B. Bereken op de algebraisch de minimale lengte van het lijnstuk AB.

Wie kan mij hiermee helpen?
Groeten
rens
Leerling bovenbouw havo-vwo - woensdag 23 maart 2005

Antwoord

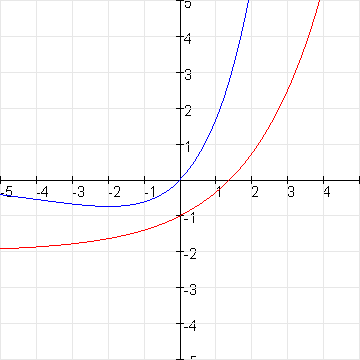
Ik veronderstel dat het gaat over de functies

f(x) = x.e^0.5x (blauw) en

g(x) = e^0.5x - 2 (rood)

De verticale rechte x = p snijdt de twee krommen in A en B. Het berekenen van de minimale lengte van AB komt neer op het bepalen voor welke waarde van x het verschil tussen de functies f(x) en g(x) minimaal is. Dus we moeten bepalen voor welke waarde van x de verticale afstand tussen f(x) en g(x) minimaal is.

We stellen h(x) = f(x) - g(x) = x.e^0.5x - (e^0.5x - 2) =
e^0.5x(x-1) + 2

Dit verschil h(x) is minimaal als de afgeleide Dh(x) gelijk is aan 0.

Dh(x) = ¹/₂.e^0.5x(x+1) en dit is gelijk aan 0 voor x = -1.

Op onderstaande grafiek zie je dat voor x = -1 de verticale afstand inderdaad het kleinst is, namelijk 0.787

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 23 maart 2005

Re: Optimaliseren