|
|
|
\require{AMSmath}



Bewijs in een driehoek
In een driehoek abc is gegeven:
ac=4·ab·cos(p/6+a/2)·cos(p/6-a/2). Bewijs: hoek Bewijs :hoek a=2·hoek c
hl
Ouder - woensdag 22 december 2004
Antwoord
Ervan uitgaande dat je met p het getal pi bedoelt...
Voorts gebruik ik graden voor de hoeken, hoofdletters voor de hoekpunten en kleine letters voor de hoeken.
Volgens één van de formules van Simpson is:
2( cos((60°+a)/2) + cos((60°-a)/2) ) = cos 60° + cos a
Zodat we hebben:
AC = 2·AB·(1/2 + cos a) = AB + 2·AB·cos a
Bekijken we nu onderstaande figuur.
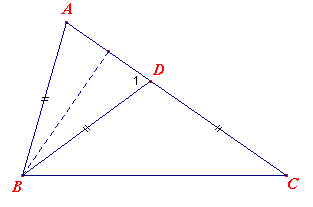
Hierin is AD = 2·AB·cos a en dus: CD = AB.
Waaruit het gestelde direct volgt, immers BD = AB en ÐD1 = 2ÐC.
Zie Formules van Simpson (MathWorld)

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 22 december 2004
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|










