WisFaq!

Bewijs in een driehoek

In een driehoek abc is gegeven:
ac=4·ab·cos(p/6+a/2)·cos(p/6-a/2). Bewijs: hoek Bewijs :hoek a=2·hoek c

hl
22-12-2004

Antwoord

Ervan uitgaande dat je met p het getal pi bedoelt...
Voorts gebruik ik graden voor de hoeken, hoofdletters voor de hoekpunten en kleine letters voor de hoeken.

Volgens één van de formules van Simpson is:
2( cos((60°+a)/2) + cos((60°-a)/2) ) = cos 60° + cos a
Zodat we hebben:
AC = 2·AB·(¹/₂ + cos a) = AB + 2·AB·cos a
Bekijken we nu onderstaande figuur.

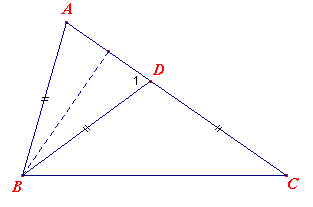
Hierin is AD = 2·AB·cos a en dus: CD = AB.
Waaruit het gestelde direct volgt, immers BD = AB en ÐD₁ = 2ÐC.

Zie Formules van Simpson (MathWorld) [http://mathworld.wolfram.com/SimpsonsFormulas.html]

dk
22-12-2004