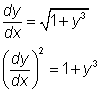|
|
|
\require{AMSmath}
Re: Welke orde en welke graad
ok, dat begrijp ik .. maar geldt dit dan ook voor andere vormen waarbij y betrokken is ? vb..
y'= sin(x-y)
is hier dan de graad van te bepalen? of geldt dit niet bij een goniometrische vorm..
maarte
Student Hoger Onderwijs België - zondag 28 september 2003
Antwoord
Ja dit geldt ook in dit geval: je kunt hier niet de graad bepalen.
Kort gezegd komt het er op neer, dat je alleen de graad van een differentiaalvergelijking kunt bepalen, als alle vormen van y en alle afgeleiden van y als veelterm geschreven zijn.
In een enkel geval kun je de vergelijking herleiden tot de gewenste vorm, zoals in het volgende voorbeeld:
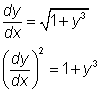
Hier is sprake van een tweedegraads eerste orde differentiaalvergelijking, omdat de hoogste afgeleide tot de tweede macht verheven staat (na herleiding).
Let op dat de derde macht van y zelf geen invloed heeft op de graad.
Ik hoop dat het zo duidelijk is.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 29 september 2003
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 14690