WisFaq!

Re: Welke orde en welke graad

ok, dat begrijp ik .. maar geldt dit dan ook voor andere vormen waarbij y betrokken is ? vb..

y'= sin(x-y)

is hier dan de graad van te bepalen? of geldt dit niet bij een goniometrische vorm..

maarten
28-9-2003

Antwoord

Ja dit geldt ook in dit geval: je kunt hier niet de graad bepalen.
Kort gezegd komt het er op neer, dat je alleen de graad van een differentiaalvergelijking kunt bepalen, als alle vormen van y en alle afgeleiden van y als veelterm geschreven zijn.
In een enkel geval kun je de vergelijking herleiden tot de gewenste vorm, zoals in het volgende voorbeeld:

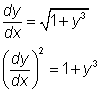
Hier is sprake van een tweedegraads eerste orde differentiaalvergelijking, omdat de hoogste afgeleide tot de tweede macht verheven staat (na herleiding).
Let op dat de derde macht van y zelf geen invloed heeft op de graad.
Ik hoop dat het zo duidelijk is.

Anneke
29-9-2003