 |
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
||||||||||||||||||
|
\require{AMSmath}



Een raaklijn door de oorsprongDe vraag luidt: In welke punten van de grafiek van de kromme met vergelijking y = x3 - 8x2 + 17x gaat de raaklijn door de oorsprong? Zelf kom ik nog tot het bepalen van de afgeleide. AntwoordEen lijn door de oorsprong heeft als vergelijking $y=ax$. Als je de lijn snijdt met de kromme en eist dat je één snijpunt krijgt?



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2025 WisFaq - versie 3
| ||||||||||||||||||


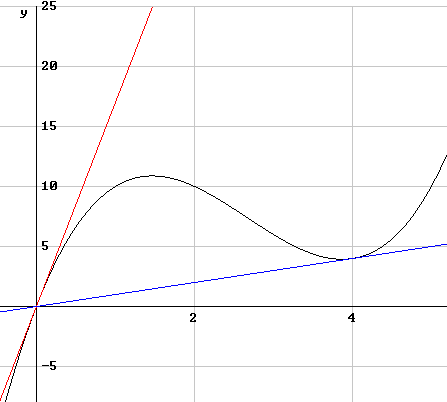


 Re: Een raaklijn door de oorsprong
Re: Een raaklijn door de oorsprong