\require{AMSmath}

Dit is een reactie op vraag 92594

Re: Poolvergelijkingen

Beste,

Dankuwel voor uw antwoord. En hoe zit het dan met deze vergelijking?

2·sin($\theta$)·cos²(2$\theta$) - 2·sin²($\theta$)·sin($\theta$) - cos($\theta$) = 0

Alvast bedankt.

nur
Student universiteit België - zondag 22 augustus 2021

Antwoord

Ik heb daar geen algemeen recept voor; soms heb je geluk en kun je dingen handig buiten de haakjes halen. Ik heb bijvoorbeeld $\cos2\theta$ vervangen door $1-2\sin^2\theta$ en toen kreeg ik dit:
$$8\sin^5\theta-10\sin^3\theta+2\sin\theta-\cos\theta=0
$$Je kunt een beetje ontbinden:
$$2\sin\theta(1-4\sin^2\theta)(1-\sin^2\theta)-\cos\theta=0
$$Door $1-\sin^2\theta=\cos^2\theta$ te gebruiken en $\cos\theta$ buiten de haakjes te halen kom ik dan op
$$\cos\theta\bigl(\sin2\theta\cdot(1-4\sin^2\theta) -1\bigr)=0
$$Dat geeft $\cos\theta=0$, dus $\theta=\frac\pi2$ en $\theta=\frac{3\pi}2$.
Wat overblijft is dit:
$$\sin2\theta\cdot(1-4\sin^2\theta)=1
$$Daar is verder niet veel mee te doen. Door wat proberen heb ik ontdekt dat $\frac{3\pi}4$ en $\frac{7\pi}4$ ook oplossingen zijn.
Hier is de grafiek van de oorspronkelijke functie.



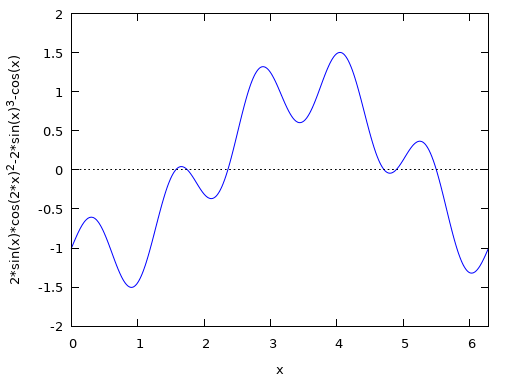
Overigens: heb je de vergelijking goed overgeschreven? Waarom staat er $2\sin^2\theta\cdot\sin\theta$ en niet gewoon $2\sin^3\theta$?

kphart
dinsdag 24 augustus 2021

©2001-2024 WisFaq