WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Randomized response

Dit is een reactie op vraag 9883

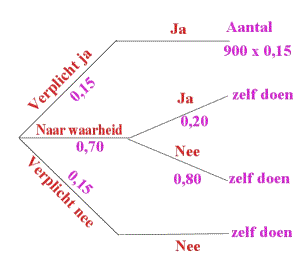
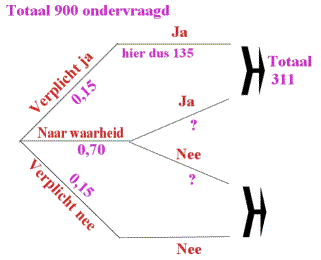
bedankt voor het antwoorden van mijn vraag. Ik denk dat ik die som heel goed kan gebruiken als bijvoorbeeld een extra bijlage (misschien dat dat nog een puntje meer opleverd), maar zou ik dan misschien ook de antwoorden mogen (ik denk dta mijn leraar die er graag bij wil). Natuurlijk heb ik het al eerst zelf even geprobeerd, maar ik kwam er niet helemaal uit (te moeilijk).
weer alvast bedankt voor alle moeite
groetjes lot
lotte
Leerling bovenbouw havo-vwo - dinsdag 15 april 2003

Antwoord

Volgens mij moet je dat ook best zelf kunnen uitrekenen. Het is telkens een kwestie van kansen berekenen en dat met 900 vermenigvuldigen. In een plaatje ziet dat er zo uit:

Bij de tweede vraag is het een kwestie van terugredeneren. Eerst die totalen even berekenen en dan doorgaan tot je de uiteindelijke gevraagde kans kunt terugrekenen. In een plaatje ziet dat er als volgt uit:

We hebben er wel vertrouwen in dat je de rest nu zelf kan vinden. Over een paar dagen zal ik de uitkomst (dus niet de hele berekening) van die tweede opgave hier nog wel eens neerzetten.

Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 16 april 2003

Re: Re: Randomized response