WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Randomized response

Ik moet een werkstuk over randomized response maken en ik vind het nogal simpel lijken. ik snap opzicht wel hoe randomized responde werkt, maar zit er ook nog een formule aan verbonden ofzo..... Ik zou graag nog wat meet wiskundige dingen laten zien, maar is dat wel mogelijk?? (ik gebruik bij de ênquete dobbelstenen, is dus ongeveer 4/6 deel naar waarheid ingevuld, toch???)Is er ook nog informatie over wie het eerste met deze methode is gekomen en waarom het zo heet???? Alvast heel erg bedankt Lot
lotte
Leerling bovenbouw havo-vwo - maandag 14 april 2003

Antwoord

Twee dingen moet je vooral benadrukken:
Waar is deze methode eigenlijk goed voor. Waarom (en in welke situaties) zou je deze methode uberhaupt toepassen.
Hoe kan ik nu toch een juiste schatting van de gezochte percentages afleiden uit mijn eindresultaten.
Randomized response betekent in feite dat aan het antwoord van de respondent een extra toevalsfactor wordt toegevoegd.

Dit jaar heb ik daar zelf eens een tentamenopgave over gegeven. Hij komt uit een (ik dacht) vwo-examen:

Pestgedrag
Om meer te weten te komen over het pestgedrag op een school wordt er een onderzoek gedaan. Aan elke leerling die aan het onderzoek meedoet, wordt de volgende vraag gesteld: pest jij wel eens?
Omdat het onderwerp gevoelig ligt, zal niet elke pester naar waarheid willen antwoorden. Daarom laat men de leerlingen antwoorden volgens de methode van randomized response. Deze methode werkt als volgt: er wordt gebruik gemaakt van een kansschijf die verdeeld is in de sectoren ja (15%), nee (15%) en naar waarheid (70%). Zie onderstaande figuur.

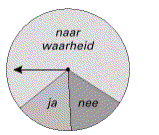
De leerling laat de wijzer van de kansschijf draaien. De wijzer komt tot stilstand in een willekeurige positie. Als de wijzer tot stilstand komt in de sector naar waarheid, moet de leerling eerlijk antwoorden. Als de wijzer in één van de andere sectoren komt, moet de leerling verplicht antwoorden wat die sector aangeeft, ongeacht of hij wel of niet pest.
Leerlingen die het antwoord „ ja” geven, doen dat om één van de volgende redenen:
- de wijzer komt in de sector „ ja” dus antwoorden ze verplicht „ ja” of
- de wijzer komt in de sector „naar waarheid ” en ze pesten wel eens.
Aan het onderzoek doen 900 leerlingen mee. Neem bij de volgende vraag aan dat 20% van deze leerlingen wel eens pest.

a. Toon aan dat dan naar verwachting 261 leerlingen „ ja” zullen antwoorden. Aanwijzing: gebruik bijvoorbeeld een kruistabel of kansboom.

b. Bij de telling blijkt dat 311 leerlingen de vraag met „ja” hebben beantwoord. Dit doet vermoeden dat het percentage leerlingen dat wel eens pest groter is dan 20%. Bereken bij welk percentage leerlingen dat wel eens pest het verwachte aantal "ja" antwoorden 311 zal zijn.

Je kunt nog veel meer doen: bijvoorbeeld bij deze methode een betrouwbaarheidsinterval voor de geschatte fractie berekenen.
Of iets zeggen over wat de invloed van de kansen bij de randomizer (de draaischijf in dit geval) op de resultaten zullen zijn. Wat gebeurt er bijvoorbeeld met zo'n betrouwbaarheidsinterval als de kans op "naar waarheid" niet 70% zou zijn maar bijvoorbeeld 40%.

Geen al te makkelijke kost maar wel leuk als je daar iets over zou kunnen zeggen. Om je een beetje op weg te helpen het volgende artikel:
Randomized response in de praktijk (Pdf)

Kom je daar niet helemaal uit, neem dan gerust weer contact op.
Met vriendelijke groet

JaDeX

Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 14 april 2003

Re: Randomized response