|
|
|
\require{AMSmath}
Overlapping bij diagonaal vouwen van een rechthoekig vel
Bij het diagonaal vouwen van een rechthoekig vel is de 'overlapping' (een gelijkbenige driehoek) afhankelijk van de verhouding lengte/breedte van de rechthoek.
Uiterste: bij vierkant (lengte=breedte) is de overlapping 100% en resteert een oppervlakte van 50%.
Hoe is de berekening bij een rechthoek?
Met dank
Jan Ka
Iets anders - donderdag 12 januari 2023
Antwoord
Hallo Jan,
Stel b=breedte van de rechthoek, en de lengte a·b met a$ \ge $ 1, zie de figuur hieronder. De oppervlakte van het totale vel is dan ab2.
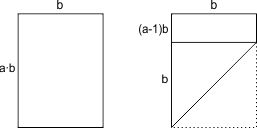
Wanneer we de korte zijde met een schuine vouw op de lange zijde vouwen, dan ontstaat een overlap in de vorm van een rechthoekige gelijkzijdige driehoek A met rechthoekszijden b, en een rechthoek B met zijden b en (a-1)b.
De oppervlakte OA van driehoek A is 0,5b2, de oppervlakte OB van rechthoek B is (a-1)b2. De bedoelde overlapping is dan:
OA/(OA+OB) = 0,5b2/(0,5b2+(a-1)b2) = 1/(2a-1).
Vermenigvuldig dit met 100 om de overlapping in procenten uit te drukken.
De resterende oppervlakte is OA+OB = 0,5b2+(a-1)b2 = (a-0,5)b2. Dit is (a-0,5)b2/(ab2)·100% van de oorspronkelijke oppervlakte, ofwel (a-0,5)/a·100%.
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 12 januari 2023
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Re: Overlapping bij diagonaal vouwen van een rechthoekig vel