|
|
|
\require{AMSmath}
Re: Sinus en cosinusregel toepassen
Hallo Willem,
Ik was op goede weg en een verhouding 1/3 diende zich aan. Verkeerd gewerkt van mij. BC zonder x had ik ook gevonden.
BC=sqrt(10-6cos(40)
BC =2,4786
Nu 2,4786/sin(40)=3/sin(C)
sin(C)= 3sin(40)/2,4786
sin(C)=0.7780
Hoek C= sin-1(0,7780)= 51°,0778°=51°04'40'
Als we nu hoek B nog uittellen komen we aan nauwelijks 16,0225 graden uit
Het antwoord zou zijn hoek C : 123°56'51'
Dit laatst antwoord is wat vreemd maar dat het een stompe hoen moet zijn ligt toch voor de hand. Of niet?
Loopt er nog wat fout of blijft mijn calculator in gebreken?
Nog een goede nacht
Rik Le
Iets anders - woensdag 18 november 2020
Antwoord
Berekening klopt wel, maar
BC$\approx$2,32459...
sin($\angle$C)$\approx$0,8295...
Ik zie zo niet wat er mis gaat.
Voorwat betreft de stompe hoek: dat volgt uit de tekening die je bij dit soort opgaven zou moeten maken...
|
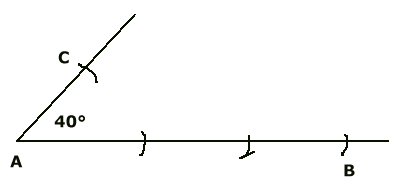
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 18 november 2020
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 90969