WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Sinus en cosinusregel toepassen

Goede avond
Volgend probleem:
Gegeven: driehoek ABC met de zijde AB als basis en c in de top.. Hoek A=40° en zijde AB is driemaal zo groot als zijde AC. Zoek de waarde van hoek C
Antwoord is: 123°56'51"

Het is een reeks van 18 oefeningen die ik vrij gemakkelijk kan oplossen en hier zit ik vast bij eentje...

Ik trachtte het volgende
BC²═=x²+9x²-6x²cos(40) (1) .
Sinusregel
x/sin(B)=3x/sin(C)
wegdelen x
geeft :
sin (C)=3 sin (B) (2)

Hoe moet het nu verder?
Kan ik nog eens op jullie rekenen??
Goede nacht

Rik Le
Iets anders - dinsdag 17 november 2020

Antwoord

Je hebt de 'werkelijke lengte' van AC en AB niet nodig. Het gaat immers om verhoudingen?

Dus ik zou zeggen;

$
\eqalign{
& BC^2 = 1^2 + 3^2 - 2 \cdot 1 \cdot 3 \cdot \cos \left( {40^\circ } \right) \cr
& BC = \sqrt {...} \cr
& \frac{{BC}}
{{\sin \left( {40^\circ } \right)}} = \frac{3}
{{\sin \left( {\angle C} \right)}} \cr}
$

Dan lukt het wel denk ik.

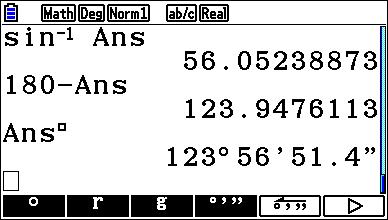
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 17 november 2020

Re: Sinus en cosinusregel toepassen