WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Examenopgave mbo 79-80 (3)

Dit is een reactie op vraag 89607

Bij de vervolg vraag(b) kom ik ook niet op een goed
antwoord.

Een lijn l heeft als vectorvoorstelling l: (1,6,3)+l(1,2,1).
Bereken de hoek tussen l en V.
Waarom krijg ik volgens deze methode en die andere van combineren verschillende vergelijkingen?

Methode 1
De normaalvector moet loodrecht op de lijn staan dus (1,2,1)(a,b,c)=0
Stel a=1 en b=1 dan c=-3 dus de vergelijking is x+y-3z=d
Of werkt dat niet zo?

Methode 2
x=1+l
y=6+2l
Z=3+l
Bovenste en onderste keer -1 en dan alles optellen geeft weer een andere vergelijking:-x+y-z=2
hiervan is de normaalvector (-1,1,-1)

Met vlak V:2x-y-2z-12=0

Krijg ik cos$\Phi$=nl·nv/|nl·nv|
=√3/9$\Rightarrow\Phi$=0,43pi in het antwoord staat 0,09 pi.
mboudd
Leerling mbo - dinsdag 14 april 2020

Antwoord

Een lijn heeft geen normaalvector. Er zijn oneindig veel richtingen die loodrecht op een lijn staan. Volgens de theorie:

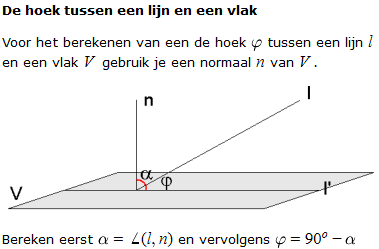
Je berekent dus de hoek tussen lijn en normaalvector van V en trek die hoek van 90° af en dan ben je er.

Het gaat dan om:

$
\begin{array}{l}
r_l = \left( {\begin{array}{*{20}c}
1 \\
2 \\
1 \\
\end{array}} \right) \\
n_V \left( {\begin{array}{*{20}c}
2 \\
{ - 1} \\
{ - 2} \\
\end{array}} \right) \\
\end{array}
$

Lukt dat dan?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 14 april 2020