WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

Re: Re: Re: Uitslag afgeknotte kegel

Dit is een reactie op vraag 60476

Kan u dit uitrekenen voor:

d₁: 150
d₂: 1000
h: 900

Dank u
Bram v
Leerling bovenbouw havo-vwo - zaterdag 21 juli 2018

Antwoord

Ok...

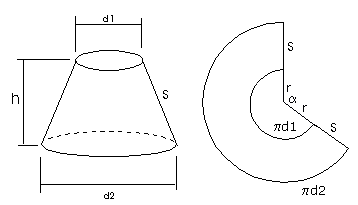
Er geldt:

$
\eqalign{s = \sqrt {\left( {\frac{{d_2 - d_1 }}
{2}} \right)^2 + h^2 }}
$

Dus in jouw geval wordt dat:

$
\eqalign{s = \sqrt {\left( {\frac{{1000 - 150}}
{2}} \right)^2 + 900^2 } = 25\sqrt {1585}}
$

Er geldt:

$
\eqalign{\frac{{r + s}}
{{d_2 }} = \frac{r}
{{d_1 }}}
$

In jouw geval wordt dat:

$
\eqalign{\frac{{r + 25\sqrt {1585} }}
{{1000}} = \frac{r}
{{150}}}
$

Als je deze vergelijking oplost dan krijg je:

$
\eqalign{r = \frac{{75\sqrt {1585} }}
{{17}}}
$

Er geldt:

$
\eqalign{\alpha = 360^o \cdot \left( {1 - \frac{{d_1 }}
{{2r}}} \right)}
$

In jouw geval wordt dat:

$
\eqalign{\alpha = 360^o \cdot \left( {1 - \frac{{150}}
{{2 \cdot \frac{{75\sqrt {1585} }}
{{17}}}}} \right) \approx 206{}^o}
$

't Is een gedoe, maar (als ik verder geen rekenfouten heb gemaakt) zou dit het moeten zijn.

Helpt dat?

Vragen naar aanleiding van dit antwoord? Klik rechts..!
zaterdag 21 juli 2018