
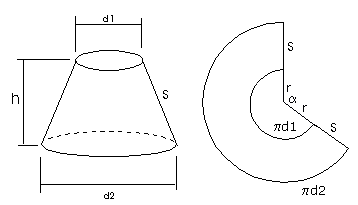
Er geldt:
$
\eqalign{s = \sqrt {\left( {\frac{{d_2 - d_1 }}
{2}} \right)^2 + h^2 }}
$
Dus in jouw geval wordt dat:
$
\eqalign{s = \sqrt {\left( {\frac{{1000 - 150}}
{2}} \right)^2 + 900^2 } = 25\sqrt {1585}}
$
Er geldt:
$
\eqalign{\frac{{r + s}}
{{d_2 }} = \frac{r}
{{d_1 }}}
$
In jouw geval wordt dat:
$
\eqalign{\frac{{r + 25\sqrt {1585} }}
{{1000}} = \frac{r}
{{150}}}
$
Als je deze vergelijking oplost dan krijg je:
$
\eqalign{r = \frac{{75\sqrt {1585} }}
{{17}}}
$
Er geldt:
$
\eqalign{\alpha = 360^o \cdot \left( {1 - \frac{{d_1 }}
{{2r}}} \right)}
$
In jouw geval wordt dat:
$
\eqalign{\alpha = 360^o \cdot \left( {1 - \frac{{150}}
{{2 \cdot \frac{{75\sqrt {1585} }}
{{17}}}}} \right) \approx 206{}^o}
$
't Is een gedoe, maar (als ik verder geen rekenfouten heb gemaakt) zou dit het moeten zijn.
Helpt dat?

WvR
21-7-2018