|
|
|
\require{AMSmath}
Re: Re: Re: Re: Re: Keerpunten berekenen
Ik had eigenlijk nog een (nieuw vraagje) hierover, ik moet ook de coördinaten berekenen van het punt met een horizontale raaklijn. Horizontale raaklijn geldt toch dat:
y'(t)=0
y(t)= 4 cost-2cos2t
y'(t)= 4 sin(2t)-4sin(t)=0
Uiteindelijk krijg je als je naar bovenstaand voorbeeld terug kijkt, dat sin(t)=0 v cos(t)=1/2
En ook dat dy/dt=0 en dx/dt$\neq$0 dat er een horizontale raaklijn is.
Voor dy heb je dus dat sin(t)=0 en voor dx= cos(t)=-1 v cos(t)=1/2 en vervolgens de t waarden ingevuld in de oorspronkelijke parametervoorstelling. Maar de coördinaten die je dan krijg, zijn dit eigenlijk dan al niet diegene die bij een horizontale raaklijn horen? Kunt u mij aub helpen?
Yvette
Iets anders - vrijdag 23 mei 2014
Antwoord
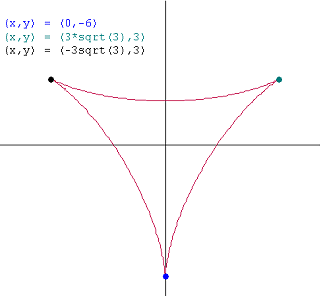
Voor een punt met horizontale raaklijn is er nog een aanvullende eis:
$\frac{dx}{dt}\neq0$
Dan blijft alleen sin(t)=0 over, dus t=0. Invullen geeft het punt $(0,2)$
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
vrijdag 23 mei 2014
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 72944