|
|
|
\require{AMSmath}
Re: Re: Re: Keerpunten berekenen
4cos(2t)+4cos(t)=0 geeft:
cos(2t)+cos(t)=0
2cos2(t)+cos(t-1)=0
cos(t)=-1 v cos (t)=0,5
Hieruit volgt: t=$\pi$+k·2$\pi$ v t= 1/3$\pi$+k·2$\pi$ v t= -1/3$\pi$+k·2$\pi$
Keerpunten: (-2,0), (2,3√3) en (2,-3√3). Doe ik dit zo goed of moet ik t anders doen? Zou u me dan aub willen helpen?
Yvette
Iets anders - maandag 12 mei 2014
Antwoord
Het lijkt er op:
4cos(2t)+4cos(t)=0
4sin(2t)-4sin(t)=0
Beide vergelijkingen oplossen geeft:
t=... (1)
t=... (2)
Zoeken naar de gemeenschappelijke waarden van t bij de oplossingen bij (1) en (2) tussen 0 en 2$\pi$ geeft dan:
t=-1/3$\pi$, t=1/3$\pi$ of t=$\pi$.
Je moet dan de t invullen in de oorspronkelijke formules!
t=$\pi$ bijvoorbeeld geeft dan:
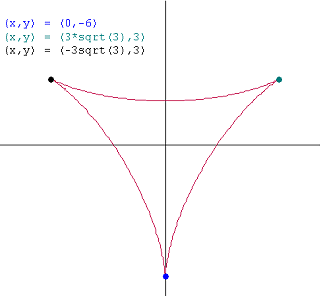
x($\pi$)= 4sin($\pi$)+2sin(2$\pi$)=0
y($\pi$)= 4cos($\pi$)-2cos(2$\pi$)=-6
Dat geeft (0,-6).
Net zo voor t=-1/3$\pi$ en t=1/3$\pi$. Je krijgt dan:
(-3√3,3) en (3√3,3)
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 12 mei 2014
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
Dit is een reactie op vraag 72619