WisFaq!

Re: Re: Re: Keerpunten berekenen

4cos(2t)+4cos(t)=0 geeft:

cos(2t)+cos(t)=0
2cos²(t)+cos(t-1)=0
cos(t)=-1 v cos (t)=0,5

Hieruit volgt: t=$\pi$+k·2$\pi$ v t= 1/3$\pi$+k·2$\pi$ v t= -1/3$\pi$+k·2$\pi$

Keerpunten: (-2,0), (2,3√3) en (2,-3√3). Doe ik dit zo goed of moet ik t anders doen? Zou u me dan aub willen helpen?

Yvette
12-5-2014

Antwoord

Het lijkt er op:

4cos(2t)+4cos(t)=0
4sin(2t)-4sin(t)=0

Beide vergelijkingen oplossen geeft:

t=... (1)
t=... (2)

Zoeken naar de gemeenschappelijke waarden van t bij de oplossingen bij (1) en (2) tussen 0 en 2$\pi$ geeft dan:

t=-¹/₃$\pi$, t=¹/₃$\pi$ of t=$\pi$.

Je moet dan de t invullen in de oorspronkelijke formules!

t=$\pi$ bijvoorbeeld geeft dan:

x($\pi$)= 4sin($\pi$)+2sin(2$\pi$)=0
y($\pi$)= 4cos($\pi$)-2cos(2$\pi$)=-6

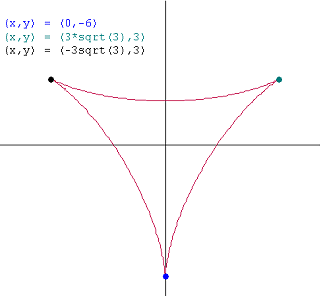
Dat geeft (0,-6).

Net zo voor t=-¹/₃$\pi$ en t=¹/₃$\pi$. Je krijgt dan:

(-3√3,3) en (3√3,3)

WvR
12-5-2014