WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

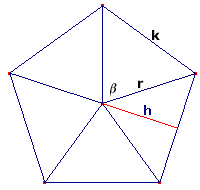
Re: Oppervlakte regelmatige vijfhoek

Dit is een reactie op vraag 50631

De oppervlakte van elk regelmatige veelhoek is de omtrek maal de helft van de loodlijn naar het zwaartepunt. Dit komt overeen met de berekening van de berekening van een cirkel $\pi$·d·¹/₄d
Jac Kn
Iets anders - woensdag 22 januari 2014

Antwoord

Dat is leuk om te weten.

$Opp = n \cdot k \cdot \frac{1}{2}h$?

Ik kan 's kijken of het overeenkomt met de formule op Oppervlakte regelmatige n-hoek:

$
\begin{array}{l}
Opp = n \cdot k \cdot \frac{1}{2}h \\
Opp = n \cdot 2r \cdot \sin \left( {\frac{\beta }{2}} \right) \cdot \frac{1}{2}r\cos \left( {\frac{\beta }{2}} \right) \\
Opp = n \cdot r^2 \cdot \sin \left( {\frac{\beta }{2}} \right) \cdot \cos \left( {\frac{\beta }{2}} \right) \\
Opp = n \cdot r^2 \cdot \frac{1}{2}\sin \left( \beta \right) \\
Opp = \frac{1}{2}n \cdot r^2 \cdot \sin \left( {\frac{{360^\circ }}{n}} \right) \\
\end{array}
$

Klopt als een bus...

Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 28 januari 2014