WisFaq!

Re: Oppervlakte regelmatige vijfhoek

De oppervlakte van elk regelmatige veelhoek is de omtrek maal de helft van de loodlijn naar het zwaartepunt. Dit komt overeen met de berekening van de berekening van een cirkel $\pi$·d·¹/₄d

Jac Knutzen
22-1-2014

Antwoord

Dat is leuk om te weten.



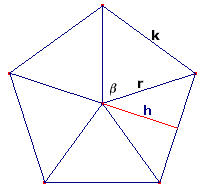
$Opp = n \cdot k \cdot \frac{1}{2}h$?

Ik kan 's kijken of het overeenkomt met de formule op Oppervlakte regelmatige n-hoek:

$
\begin{array}{l}
Opp = n \cdot k \cdot \frac{1}{2}h \\
Opp = n \cdot 2r \cdot \sin \left( {\frac{\beta }{2}} \right) \cdot \frac{1}{2}r\cos \left( {\frac{\beta }{2}} \right) \\
Opp = n \cdot r^2 \cdot \sin \left( {\frac{\beta }{2}} \right) \cdot \cos \left( {\frac{\beta }{2}} \right) \\
Opp = n \cdot r^2 \cdot \frac{1}{2}\sin \left( \beta \right) \\
Opp = \frac{1}{2}n \cdot r^2 \cdot \sin \left( {\frac{{360^\circ }}{n}} \right) \\
\end{array}
$

Klopt als een bus...

WvR
28-1-2014