|
|
|
\require{AMSmath}



Kortste routes bepalen
De volgende opgave staat in math for all opgave 12 tekening 2:
Math4all-d15-print-lt.html
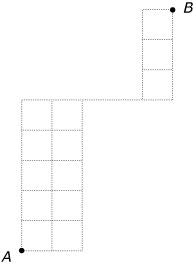
Hoeveel kortste routes zijn er mogelijk in deze roosters van punt A naar punt B?
1. (7,2)·(6,3)
2. (7,2)·(4,1) maar het antwoord was (7,2)·(4,3) ?
bouddo
Leerling mbo - maandag 13 augustus 2012
Antwoord
Goed opgemerkt, maar 1 keer 'rechts' kiezen uit 4 is toch hetzelfde als 3 keer 'omhoog' kiezen uit 4? Meer in 't algemeen kan je stellen:
$
\left( {\begin{array}{*{20}c}
n \\
k \\
\end{array}} \right) = \left( {\begin{array}{*{20}c}
n \\
{n - k} \\
\end{array}} \right)
$
Een bewijs is te doen...
Volgens de definitie:
$
\left( {\begin{array}{*{20}c}
n \\
k \\
\end{array}} \right) = \frac{{n!}}{{k! \cdot \left( {n - k} \right)!}}
$
Dus:
$
\left( {\begin{array}{*{20}c}
n \\
{n - k} \\
\end{array}} \right) = \frac{{n!}}{{\left( {n - k} \right)! \cdot \left( {n - \left( {n - k} \right)} \right)!}} = \frac{{n!}}{{(n - k)! \cdot k!}}
$
Wiskunde is cool...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
dinsdag 14 augustus 2012
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











