|
|
|
\require{AMSmath}



Ongelijkheid oplossen
Ik moet de volgende ongelijkheid oplossen:
4+2x/(x-1)$\leq$3
eerst gelijkstellen geeft:
3(x-1)=4+2x
3x-3=4+2x
x=7
dus:
4+2x/(x-1)$\leq$3 dan x$\geq$7
Maar het antwoordmodel geeft x$\leq$1 ook als oplossing die kan ik niet vinden.
bouddo
Leerling mbo - maandag 9 april 2012
Antwoord
Zo los je geen ongelijkheid op, maar zo:
$
\large\begin{array}{l}
\frac{{4 + 2x}}{{x - 1}} \le 3 \\
\frac{{4 + 2x}}{{x - 1}} - 3 \le 0 \\
\frac{{4 + 2x}}{{x - 1}} - 3 \cdot \frac{{x - 1}}{{x - 1}} \le 0 \\
\frac{{4 + 2x}}{{x - 1}} - \frac{{3x - 3}}{{x - 1}} \le 0 \\
\frac{{4 + 2x - 3x + 3}}{{x - 1}} \le 0 \\
\frac{{7 - x}}{{x - 1}} \le 0 \\
\end{array}
$
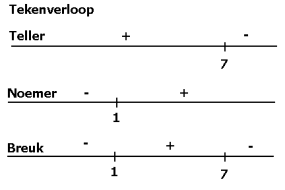
De oplossing is x$<$1 of x$\geq$7
Jaja... werk aan de winkel.
Zie ook Het oplossen van ongelijkheden

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
maandag 9 april 2012
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|











