WisFaq!

Ongelijkheid oplossen

Ik moet de volgende ongelijkheid oplossen:
4+2x/(x-1)$\leq$3

eerst gelijkstellen geeft:
3(x-1)=4+2x
3x-3=4+2x
x=7
dus:
4+2x/(x-1)$\leq$3 dan x$\geq$7

Maar het antwoordmodel geeft x$\leq$1 ook als oplossing die kan ik niet vinden.

bouddou
9-4-2012

Antwoord

Zo los je geen ongelijkheid op, maar zo:

$
\large\begin{array}{l}
\frac{{4 + 2x}}{{x - 1}} \le 3 \\
\frac{{4 + 2x}}{{x - 1}} - 3 \le 0 \\
\frac{{4 + 2x}}{{x - 1}} - 3 \cdot \frac{{x - 1}}{{x - 1}} \le 0 \\
\frac{{4 + 2x}}{{x - 1}} - \frac{{3x - 3}}{{x - 1}} \le 0 \\
\frac{{4 + 2x - 3x + 3}}{{x - 1}} \le 0 \\
\frac{{7 - x}}{{x - 1}} \le 0 \\
\end{array}
$



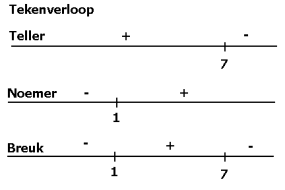
De oplossing is x$<$1 of x$\geq$7

Jaja... werk aan de winkel.

Zie ook Het oplossen van ongelijkheden

WvR
9-4-2012