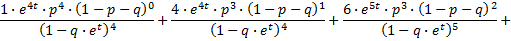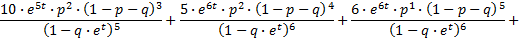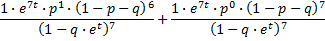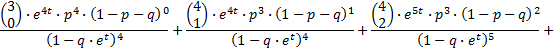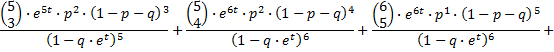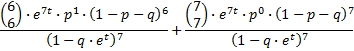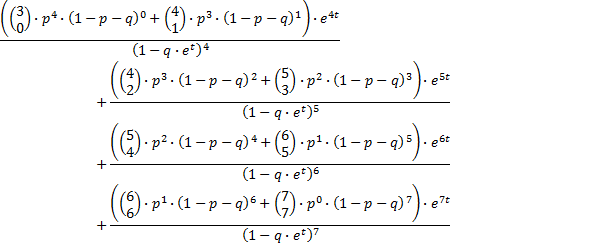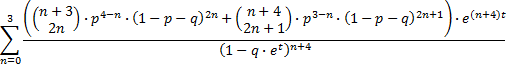|
|
|
\require{AMSmath}
Een formule vereenvoudigen met het sommatieteken
Ik heb de volgende formule:
exp(4*t)*p^4/(1-exp(t)*q)^4+4*exp(4*t)*p^3*(1-p-q)/(1-exp(t)*q)^4+6*exp(5*t)*p^3*(1-p-q)^2/(1-exp(t)*q)^5+10*exp(5*t)*p^2*(1-p-q)^3/(1-exp(t)*q)^5+5*exp(6*t)*p^2*(1-p-q)^4/(1-exp(t)*q)^6+6*exp(6*t)*p*(1-p-q)^5/(1-exp(t)*q)^6+exp(7*t)*p*(1-p-q)^6/(1-exp(t)*q)^7+exp(7*t)*(1-p-q)^7/(1-exp(t)*q)^7
Het lijkt me, dat je de formule m.b.v. het sommatieteken als één formule kunt schrijven. Ik heb vooral moeite met de coëfficiënten 1, 4, 6, 10, 5, 6, 1, 1.
Zoudt U me willen helpen?
Ad van
Iets anders - zaterdag 13 augustus 2011
Antwoord
Beste Ad,
Dit is wel een gaaf puzzeltje!
Als ik de formule juist begrijp, staat er:
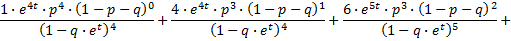
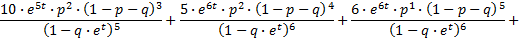
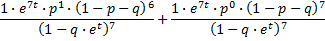
De coëfficiënten 1, 4, 6, 10, 5, 6, 1, 1 komen uit de driehoek van Pascal en zijn dus binomiaalcoëfficiënten. In jouw formule:
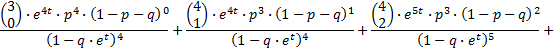
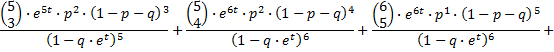
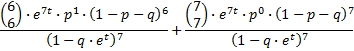
Als je nu de termen met gelijke noemer samenneemt, krijg je:
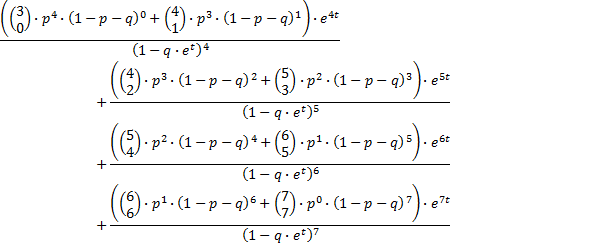
en dat is niet zo moeilijk onder een sommatieteken te brengen, bijvoorbeeld:
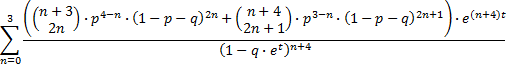
KLY
|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 14 augustus 2011
|
|
home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|
