WisFaq!

Een formule vereenvoudigen met het sommatieteken

Ik heb de volgende formule:

exp(4*t)*p^4/(1-exp(t)*q)^4+4*exp(4*t)*p^3*(1-p-q)/(1-exp(t)*q)^4+6*exp(5*t)*p^3*(1-p-q)^2/(1-exp(t)*q)^5+10*exp(5*t)*p^2*(1-p-q)^3/(1-exp(t)*q)^5+5*exp(6*t)*p^2*(1-p-q)^4/(1-exp(t)*q)^6+6*exp(6*t)*p*(1-p-q)^5/(1-exp(t)*q)^6+exp(7*t)*p*(1-p-q)^6/(1-exp(t)*q)^7+exp(7*t)*(1-p-q)^7/(1-exp(t)*q)^7

Het lijkt me, dat je de formule m.b.v. het sommatieteken als één formule kunt schrijven. Ik heb vooral moeite met de coëfficiënten 1, 4, 6, 10, 5, 6, 1, 1.

Zoudt U me willen helpen?

Ad van der Ven
13-8-2011

Antwoord

Beste Ad,

Dit is wel een gaaf puzzeltje!

Als ik de formule juist begrijp, staat er:





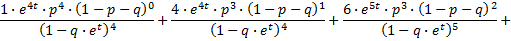
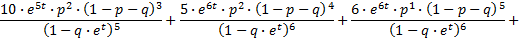
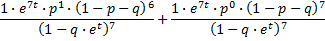
De coëfficiënten 1, 4, 6, 10, 5, 6, 1, 1 komen uit de driehoek van Pascal en zijn dus binomiaalcoëfficiënten. In jouw formule:





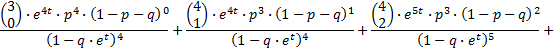
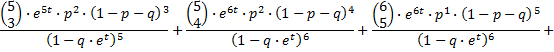
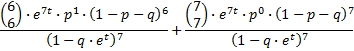
Als je nu de termen met gelijke noemer samenneemt, krijg je:



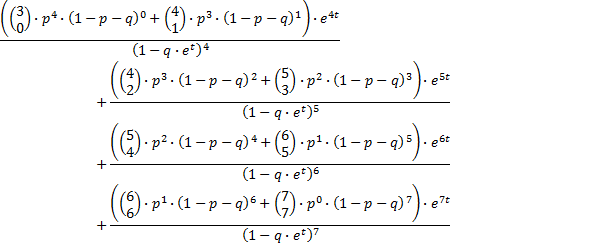
en dat is niet zo moeilijk onder een sommatieteken te brengen, bijvoorbeeld:

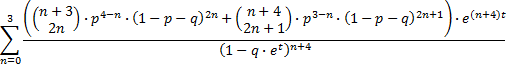
KLY
14-8-2011