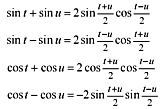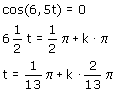|
|
|
\require{AMSmath}



Herleiden
Hallo,
Ik heb nogal moeite met goniometrie, voornamelijk bij vragen waarbij je formules moet herleiden. Zo kom ik niet goed uit de volgende vraag:
De beweging van een punt in het Oxy-vlak wordt voor 0 t t 2p gegeven door: 2p gegeven door:
x = cos 15t + cos 2t
y = sin15t + sin 2t
a. Toon aan, dat de bewegingsvergelijkingen kunnen worden herleid tot
x = 2 cos (6,5t) · cos (8,5t)
y = 2 cos (6,5t) · sin (8,5t)
b. Bij het doorlopen van de baan voor 0  t t  2p passeert het punt een aantal keren (0,0). Bereken dit langs algebraļsche weg. 2p passeert het punt een aantal keren (0,0). Bereken dit langs algebraļsche weg.
Vooral de laatste vraag vind ik lastig. Is hier ook een stappenplan voor of iets dergelijks?
Alvast bedankt voor de hulp,
Margot
Margot
Leerling bovenbouw havo-vwo - zondag 13 januari 2008
Antwoord
Op je formulekaart staat een aantal somformules...
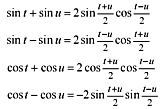
Nu moet gelden dat:
2cos(6,5t)·cos(8,5t)=0
2cos(6,5t)·sin(8,5t)=0
Wanneer is dat nu het geval!?
Als cos(6,5t)=0 dus:
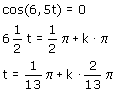
Zie 6. Goniometrische vergelijkingen oplossen
Daarmee zou het (zonder al te veel moeite) moeten lukken, hoop ik...

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
zondag 13 januari 2008
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|








 t
t