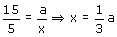WisFaq!

De digitale vraagbaak voor het wiskundeonderwijs

HOME

samengevat

\require{AMSmath}

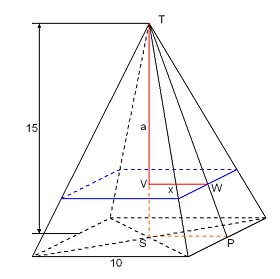
Inhoudsberekening aan integraal

Een piramide T.ABCD heeft een vierkant grondvlak van 10 bij 10. De top T ligt recht boven het midden M van het grondvlak. De hoogte is TM=15. De inhoud van de piramide is als goed is ¹/₃·15·100.

Maar bij het vervolg van de vraag komt er op afstand a van de top een vierkant PQRS. Nu moet ik uitleggen dat PQ=²/₃a is en de oppervlakte van vierkant PQRS uitdrukken in a. Hoe doe ik dit?
Pascal
Leerling bovenbouw havo-vwo - woensdag 3 januari 2007

Antwoord

De letters kloppen niet helemaal maar 't maakt het, denk ik, wel duidelijk:

In driehoek SPT geldt:

Denk aan gelijkvormigheid! Waarmee jouw PQ=²/₃a.

De oppervlakte van het vierkant is dan gelijk aan ⁴/₉a².

Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 3 januari 2007