
Inhoudsberekening aan integraal
Een piramide T.ABCD heeft een vierkant grondvlak van 10 bij 10. De top T ligt recht boven het midden M van het grondvlak. De hoogte is TM=15. De inhoud van de piramide is als goed is 1/3·15·100.
Maar bij het vervolg van de vraag komt er op afstand a van de top een vierkant PQRS. Nu moet ik uitleggen dat PQ=2/3a is en de oppervlakte van vierkant PQRS uitdrukken in a. Hoe doe ik dit?
Pascal
Leerling bovenbouw havo-vwo - woensdag 3 januari 2007
Antwoord
De letters kloppen niet helemaal maar 't maakt het, denk ik, wel duidelijk:
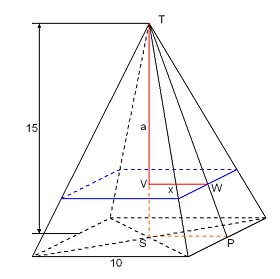
In driehoek SPT geldt:
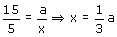
Denk aan gelijkvormigheid! Waarmee jouw PQ=2/3a.
De oppervlakte van het vierkant is dan gelijk aan 4/9a2.

woensdag 3 januari 2007
 ©2001-2024 WisFaq
©2001-2024 WisFaq
|