|
|
|
\require{AMSmath}



Herleiden tot hoeken in het eerste kwadrant
Goedemorgen,
Vanuit vrijwel géén theorie moet ik een aantal series herleiden tot hoeken in het eerste kwadrant: sin(4/3$\pi$), tan(-1/4$\pi$), cos(5/6$\pi$).
Ik heb echter geen idee waar te beginnen! Zouden jullie er wellicht één of twee kunnen oplossen en mij links kunnen geven naar additionele theorie omtrent dit onderdeel van goniometrie?
Alvast bedankt!
Peter
Peter
Student universiteit - woensdag 2 augustus 2006
Antwoord
Je zou de formules onder 2. op 6. Goniometrische vergelijkingen oplossen even eigen kunnen maken natuurlijk...
Maar je kan natuurlijk gewoon naar de grafieken kijken!
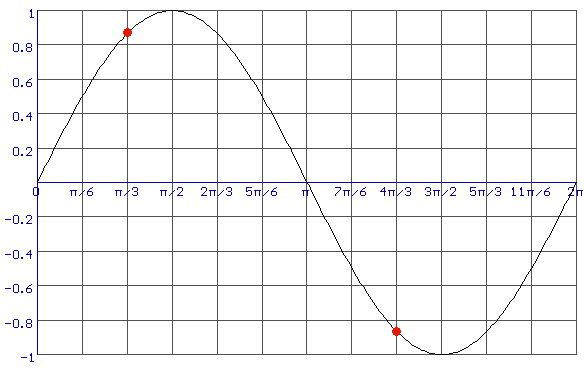
Je ziet sin(11/3$\pi$)=-sin(1/3$\pi$)
Nog maar één dan...
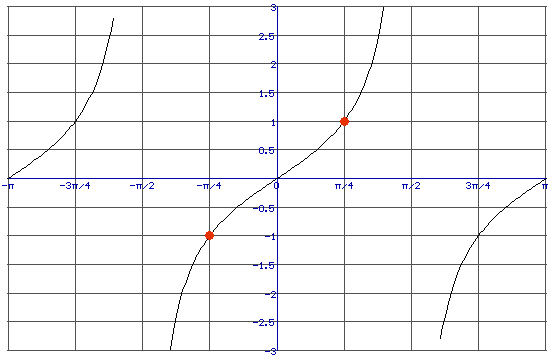
Je ziet tan(-1/4$\pi$)=-tan(1/4$\pi$)
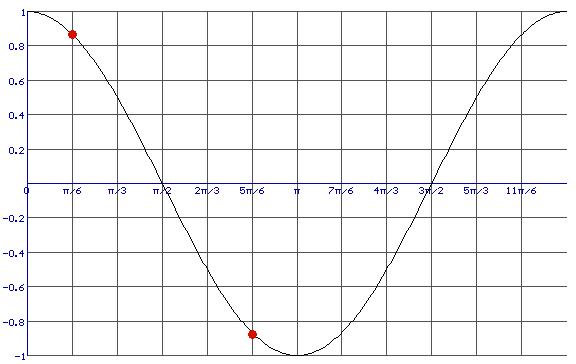
..en cos(5/6$\pi$)=-cos(1/6$\pi$)
't Een en ander zou natuurlijk ook kunnen met de eenheidscirkel.

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
woensdag 2 augustus 2006
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2024 WisFaq - versie 3
|












