|
|
|
\require{AMSmath}



Re: Re: Meetkplaats complex getal
hallo TOM,
Als ik de uitwerking maak en de noemer met de toegevoegde vermenigvuldig met zijn toegevoegde(geconjugeerde) dan krijg ik:
(x+yi-1)2/(x+yi)2-1= (x2-y2+1+2xyi-2x-2yi)/(x2-y2-1+2xyi)=0
Nu is het reële deel in de teller gelijk nul en krijgen we
x2-y2-2x+1=0 Welke kegelsnede moet ik mij daarbij voorstellen dan? of (x-1)2-y2=0.
Het antwoord moet zijn :het deel van de cirkel C(o,1) dat boven de reële as ligt.
Dank U voor uw geduld
Rik
lemmen
Ouder - donderdag 15 december 2005
Antwoord
Beste Rik,
Die "-2x" is er volges mij teveel aan. We vermenigvuldigen ook net met de toegevoegde uitdrukking om de noemer reëel te krijgen, daar mag dus geen i meer in voorkomen!
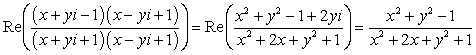
Dit is zonder al teveel tussenstappen, reken zelf evt na. Om dit reëel deel 0 te krijgen moet de teller 0 zijn (en de noemer verschillend van 0).
We vinden dus x2+y2-1 = 0 Û x2 + y2 = 1, precies de eenheidscirkel.
Herinner je echter dat de tangens meerdere oplossingen geeft, ook die met een veelvoud p. In de onderste helft van deze cirkel zal het argument telkens -p/2 zijn, vandaar dat de oplossing enkel het gedeelte van de cirkel C(O,1) is waarvoor y  0 of dus Im(z) 0 of dus Im(z)  0. 0.
mvg,
Tom

|
Vragen naar aanleiding van dit antwoord? Klik rechts..!
donderdag 15 december 2005
|

|



home |
vandaag |
bijzonder |
gastenboek |
statistieken |
wie is wie? |
verhalen |
colofon
©2001-2025 WisFaq - versie 3

|








 Dit is een reactie op vraag 42317
Dit is een reactie op vraag 42317 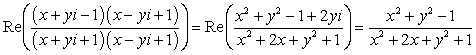
 0 of dus Im(z)
0 of dus Im(z) 
