 |
De digitale vraagbaak voor het wiskundeonderwijshome | vandaag | gisteren | bijzonder | gastenboek | wie is wie? | verhalen | contact |
|||||||||||||||||
|
\require{AMSmath}



Kwadraatafsplitsen bij de formule om de top van een parabool te vindenHoe kan je door middel van kwadraatafsplitsen van ax2+bx+c komen tot de formule om de top van een parabool te berekenen (-b/2a? Antwoord



home | vandaag | bijzonder | gastenboek | statistieken | wie is wie? | verhalen | colofon ©2001-2024 WisFaq - versie 3
| |||||||||||||||||

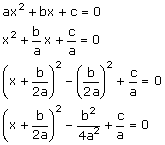
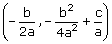 .
.
